(Update: 1/19/2009 Check out my lastest computation of 14.9 billion digits.)
On December 8, 2006, I successfully computed and verified the Euler-Mascheroni Constant to 116,580,041 digits using a medium performance laptop.
The Euler-Mascheroni Constant is denoted using the symbol γ and has a numerical value of
γ = 0.57721566490153286060651209008240243104215933593992...
The run-times were:
The digits can be downloaded in the following links.
Two computations were performed using independent methods and the results matched up to 116,580,041 digits.
The laptop used for both computations was a Toshiba Satellite A105-A4074 that had the following specifications.
The algorithm used for computation was the Brent-McMillan Formula used with Binary Splitting. Both are described in detail here. The computation used a cutting parameter of n = 225 with the precision carried out to about 117.7 million digits. Verification was done using the same approach but with n = 226 with the same carry precision. The two results matched up to 116,580,041 decimal digits.
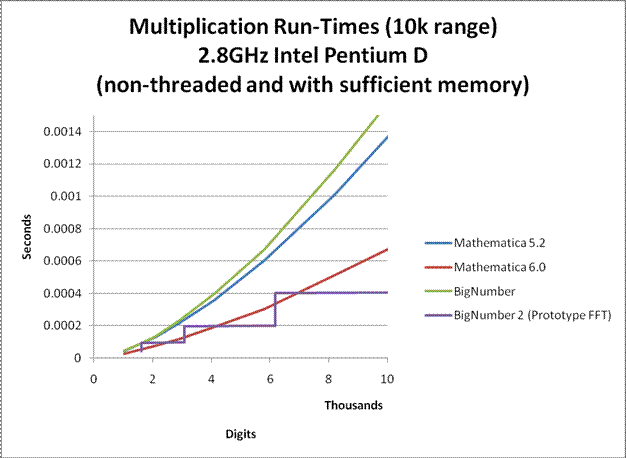
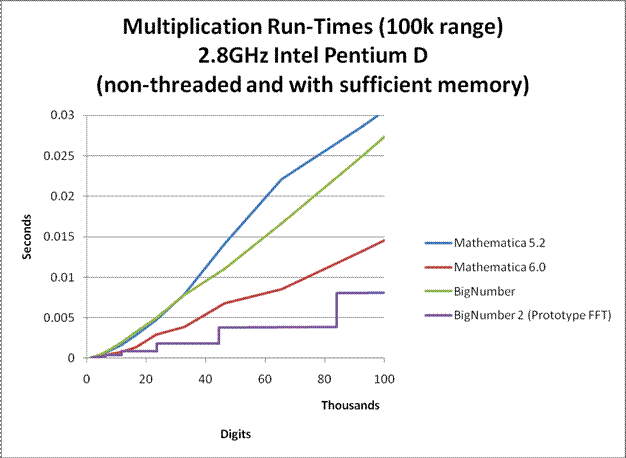
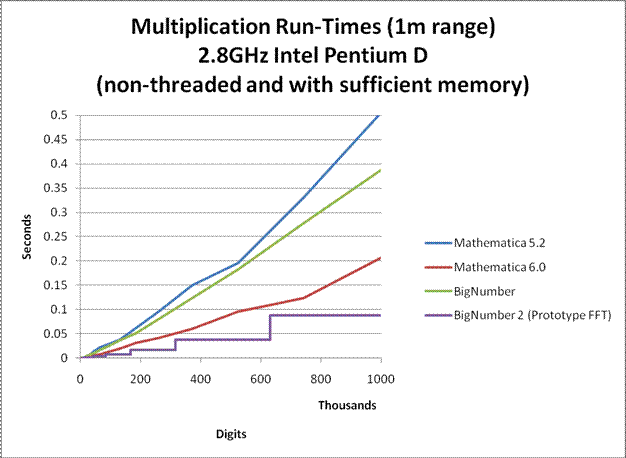
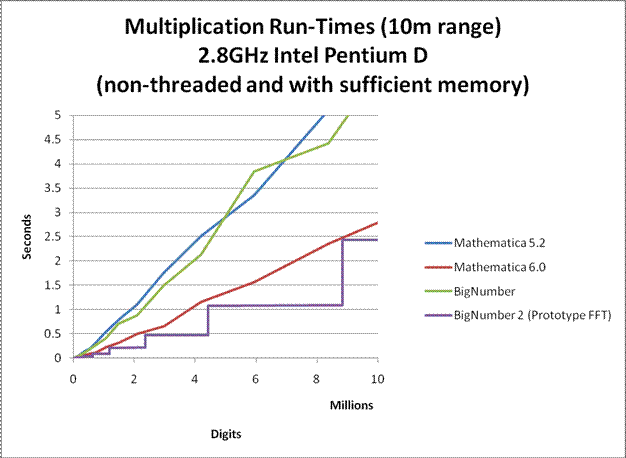
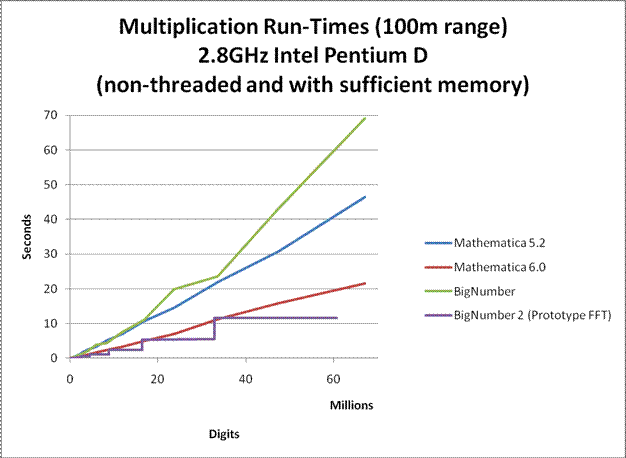
In order to allow the computation to be performed on a personal laptop in a reasonable amount of time, many speed and memory optimizations have been performed on the program. For large precisions, it can sometimes compute Euler's Constant more than 3 times faster than all commercial number-crunching programs that I know of. Nevertheless, the program is far from optimal. The multiplication algorithm used for large products was an unoptimized Fermat Number Transform (FNT) approach similar to the one used in GMP. Not only is the implementation unoptimized, the FNT algorithm itself is very slow compared to a well optimized Fast Fourier Transform (FFT) approach. Furthermore, no assembly optimizations were performed. Nevertheless, the multiplication that was used had run-times comparable to that of Mathematica 5.2. (see graphs below)
If a well optimized FFT multiplication is to be used instead, run-time can be improved by a factor of 4. If efficient FFT caching is also used, run-time can be improved by up to a factor of 10. A final minute improvement could be to rewrite the entire program in C as opposed to a combination of C and java to eliminate JNI overheads. (UPDATE 2/7/2008: I have finally completed a prototype FFT. See graphs below.)
Here are some graphs comparing the multiplication speeds at various sizes. Click on them to enlarge.
Notes:
BigNumber is the temporary name given to library that was used for this computation. (BigNumber is the one used for this computation, while BigNumber 2 is a new development.)
To my knowledge, Mathematica probably uses GMP for it's arithmetic. So the plots for Mathematica may also apply to the versions of GMP that they use. (Although I do not know which versions of GMP it uses, my guess is that Mathematica 5.2 uses GMP 4.1.4 and Mathematica 6 uses GMP 4.2.1.)
Using n = 225, the maximum number of digits that can be obtained is approximately 116.5 million digits. Using n = 226 the limit is about 233.1 million digits. Therefore, the first computation correctly produced only 116.5 million digits even though the precision was set at 117.7 million digits. However, the second computation (most likely) produced 117.7 million digits. Of course, comparing the files only verifies the first 116.5 million digits.
It is likely that the second computation correctly produced 117.7 million digits (minus a negligible amount of rounding error), but, as of this writing, the last 1.2 million digits have not been verified.
I would like to thank Mr. Scott Friedland for teaching me valuable materials needed for writing this program. I would like to give special thanks Raymond Chan for helping me test the program and Cameron Tacklind for hosting this page for so long before it was moved here. Furthermore, I would like to thank Professor Robert Dick and Professor Russ Joseph for their guidance and encouragements and for giving me access to a supercomputer (although later I found it was not needed). Finally, I would like to thank all the people in my dorm who cheered me on.
Contact me via e-mail. I'm pretty good with responding unless it gets caught in my school's junk mail filter.