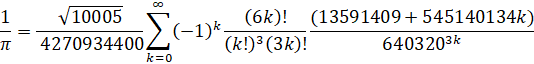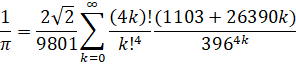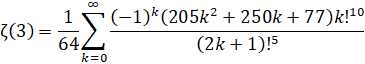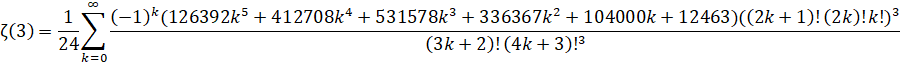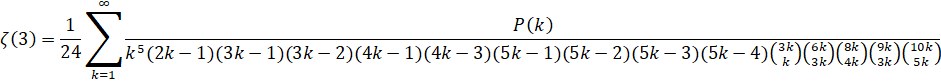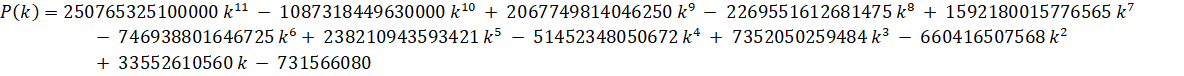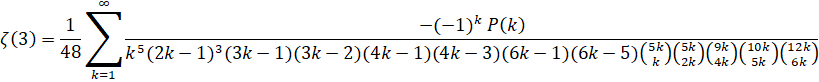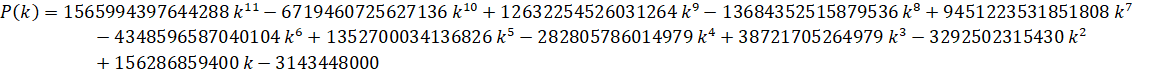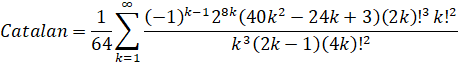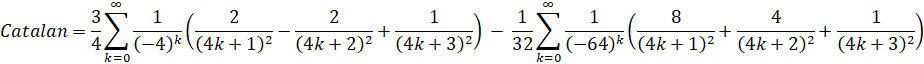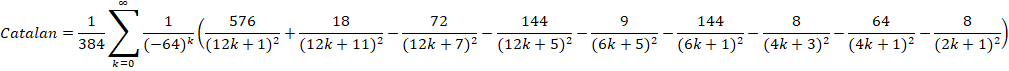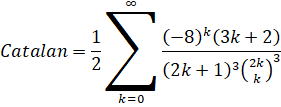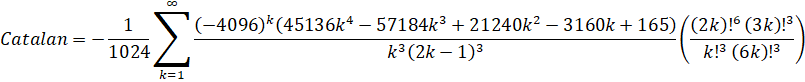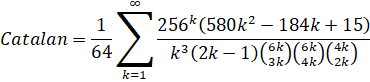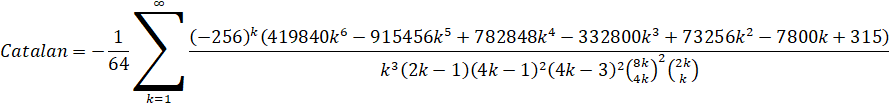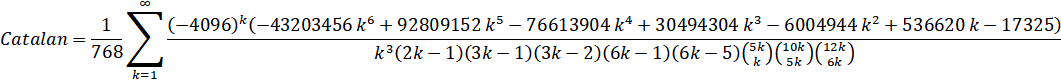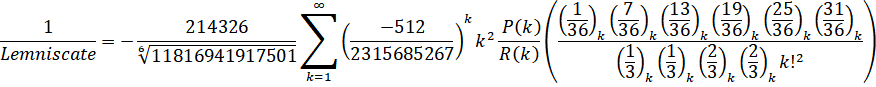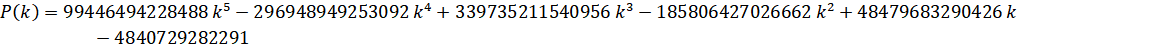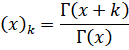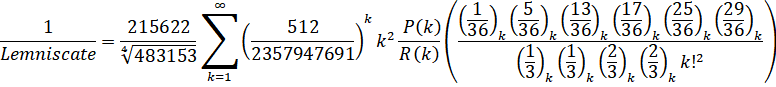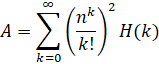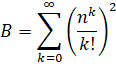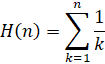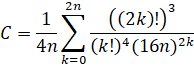Formulas and Algorithms
By Alexander Yee
(Last updated: May 14, 2019)
Back To:
y-cruncher has two algorithms for each major constant that it can compute - one for computation, and one for verification. The constants are listed here in approximate order ascending difficulty to compute.
All complexities shown assume multiplication to be O(n log(n)). It is slightly higher than that, but for all practical purposes, O(n log(n)) is close enough.
Square Root of n and Golden Ratio
1st order Newton's Method - Runtime Complexity: O(n log(n))
Note that the final radix conversion from binary to decimal has a complexity of O(n log(n)2).
There are no secondary formulas for either sqrt(n) or the Golden Ratio. Verification can be trivially done as:
- sqrt(2) and sqrt(200) are the same but the digits shifted over by 1.
- Golden Ratio and sqrt(125) are also essentially the same.
These square root constants are extremely fast to compute. It actually takes longer to convert the binary digits to decimal.
Taylor Series of exp(1): O(n log(n)2)
Taylor Series of exp(-1): O(n log(n)2)
Chudnovsky (1988): O(n log(n)3)
Ramanujan's (1910): O(n log(n)3)
References:
ArcCoth(n) - Inverse Hyperbolic Cotangent
Straightforward Taylor Series. Nothing special here.
This isn't intended to be a "real" constant. It's used internally by log(n) and is exposed to the user.
Machin-Like Formulas: O(n log(n)3)
Starting from v0.6.1, y-cruncher is able to generate and utilize machin-like formulas for the log of any small integer.
Generation of machin-like formulas for log(n) is done using table-lookup along with a branch-and-bound search on several argument reduction formulas.
References:
There doesn't seem to be good record of who discovered which of the formulas above. Most of them are fairly easy to generate anyway. So it's likely these have been independently rediscovered by many people. The log(3) formula here was generated by y-cruncher.
Wedeniwski (1998): O(n log(n)3)
Amdeberhan-Zeilberger (1997): O(n log(n)3)
References:
Catalan has historically been one of the slowest constants to compute. But recently discovered formulas by Guillera, and Pilehrood has changed this. Thanks to these newer formulas, Catalan's Constant is now almost as fast to compute as Zeta(3).
Lupas (2000): O(n log(n)3)
Huvent (2006): O(n log(n)3)
y-cruncher uses the following rearrangement of Huvent's formula:
Guillera (2008): O(n log(n)3
Guillera (2019): O(n log(n)3) - (ETA: y-cruncher v0.7.8)
Pilehrood (2010-short): O(n log(n)3)
Pilehrood (2010-long): O(n log(n)3)
References:
Gauss Formula: O(n log(n)3)
Sebah's Formula: O(n log(n)3)
Note that the AGM-based algorithms are probably faster. But y-cruncher currently uses these series-based formulas because:
- It lacks an implementation of sqrt(N) for arbitrary N. It only supports N being a small integer.
- There already is a series summation framework that can be easily applied to the ArcSinlemn() function.
References:
Brent-McMillan (alone): O(n log(n)3)
Brent-McMillan with Refinement: O(n log(n)3)
References:
Note that both of these formulas are the same with the only difference being the refinement term. Therefore, in order for two computations to be independent enough to qualify as a verified record, they must be done using different n regardless of whether the refinement term is used.
Of all the things that y-cruncher supports, the Euler-Mascheroni Constant is the slowest to compute and by far the most difficult to implement. So it suitably finds itself at the bottom of this list. A short list of things that make it difficult:
- The Brent-McMillan algorithm is not a single formula, but rather a class of formulas that give successively better approximations. So the series is different depending on the desired precision.
- Series A is a double summation due to the harmonic series. This makes it very difficult to derive a Binary Splitting recursion for it. And once found, it is significantly more complicated than that of the other constants.
- Series A, B, and C all have irregular and non-linear convergence behavior.
- Series C is divergent.
- As of 2018, the only other known efficient algorithm is the class of algorithms based on Sweeney's Method. While these methods are easier to implement, they are slower and require excess precision due to destructive cancellation.
y-cruncher only uses n that are powers of two. This simplifies the implementation in many ways as well as lending itself to a multitude of shift optimizations.
The Euler-Mascheroni Constant has a special place in y-cruncher. It is one of the first constants to be supported (even before Pi) and it is among the first for which a world record was set using y-cruncher. As such, y-cruncher derives its name from the gamma symbol for the Euler-Mascheroni Constant.
Series Summation:
Most of the formulas above involve an infinite series of some sort. These are done using standard Binary Splitting techniques with the following catches:
- Precision is tightly controlled to keep operands from becoming unnecessarily large.
- The cutting points for the binary splitting recursions are usually significantly skewed in order to reduce memory usage and improve load-balance.
- Series summation is partially done backwards. The lowest terms (terms with the largest index) are summed first. The motivation and details for this is quite intricate and goes hand-and-hand with the skewing. So I won't go into that.
This series summation scheme (including the skewed splitting and backwards summing) has been the same in all versions of y-cruncher to date. All of this is expected to change when GCD factorization is to be incorporated.