5 Trillion Digits of Pi - New World Record
Pushing the limits of personal computing... How much further can we go?
By Alexander J. Yee & Shigeru Kondo
(Last updated: September 22, 2016)
For anyone who is interested, this was recently the topic of a Stack Overflow question that I answered.
October 17, 2011: The record has been improved to 10 trillion digits.
This is a followup to our previous announcement of our computation of 5 trillion digits of Pi. This article details some of the methods that were used for the computation as well as the hardware and the full timeline of the computation.
Some of you knew this was coming... It was just a matter of when. (and how many digits)
Although we were very quiet about this computation while it was running, anyone who followed my website or my XtremeSystems thread between February and May would have easily guessed that we were attempting a world record.
|
Shortcuts:
|
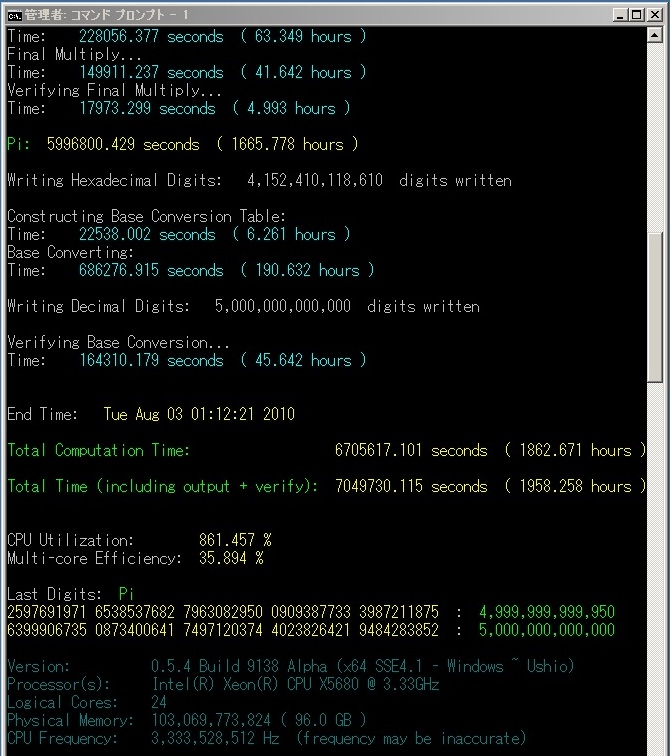
Computation Statistics - All times are Japan Standard Time (JST).
Here are the full computation statistics. As with all significant computations that are done using y-cruncher - A Multi-Threaded Pi Program, a screenshot and validation is included. Since the computation was done in multiple sessions, there is no single screenshot that captures the entire computation from start to finish. The screenshot provided here is simply the one that shows the greater portion of the computation.
The main computation took 90 days on Shigeru Kondo's desktop. The computer was dedicated for this task.
Over the course of the computation, one error was detected and corrected via software ECC. Since the error was corrected, the final results are not affected. The computation error is believed to be caused by a hardware anomaly, or by hardware instability.
Due to the size of this computation, a tremendous amount of memory was needed:
If the digits were stored in an uncompressed ascii text file, the combined size of the decimal and hexadecimal digits would be 8.32 TB.
*All units used in this article are binary: GB = 230 bytes TB = 240 bytes
Validation File: Validation - Pi - 5,000,000,000,000.txt |
|
*The total time also includes the time needed to output the digits to disk as well as the time needed to recover from the computational error.
For a detailed timeline of events related to this computation, see here.
Because it's Pi... and because we can!
On a more serious note:
After Fabrice Bellard's announcement of 2.7 trillion digits on a "relatively cheap" desktop, it was pretty clear that the limit of personal computing was a lot higher.
Shigeru Kondo and I wanted to see how much better we could do if we used some more powerful hardware.
Both of us are hardware fanatics. And both of us (especially Shigeru Kondo) had some very powerful machines at our disposal.
So with that, we decided to see how far we could push the limits of personal computing using personally owned hardware.
Unlike Fabrice Bellard's record which focused on efficiency and getting the most out of a small amount of hardware. Our computation focused more on getting the most performance and scalability from a LOT of hardware.
How much hardware can we cram into one machine and still make it faster?
The main challenge for a computation of such a size, is that both software and hardware are pushed beyond their limits.
For such a long computation and with so much hardware, failure is not just a probability. It is a given. There are simply too many components that can fail.
So the questions become:
- How much can the hardware be expanded while maintaining an acceptable level of reliability?
- Is it possible to build enough fault-tolerance into the software to cover for hardware failure?
Hardware: Shigeru Kondo's Desktop
Shigeru Kondo's computer had the following specifications:
- Processor
- 2 x Intel Xeon X5680 @ 3.33 GHz - (12 physical cores, 24 hyperthreaded)
- Memory
- 96 GB DDR3 @ 1066 MHz - (12 x 8 GB - 6 channels) - Samsung (M393B1K70BH1)
- Motherboard
- Asus Z8PE-D12
- Hard Drives
- 1 TB SATA II (Boot drive) - Hitachi (HDS721010CLA332)
3 x 2 TB SATA II (Store Pi Output) - Seagate (ST32000542AS)
16 x 2 TB SATA II (Computation) - Seagate (ST32000641AS) - Raid Controller
- 2 x LSI MegaRaid SAS 9260-8i
- Operating System
- Windows Server 2008 R2 Enterprise x64
- Built By
- Shigeru Kondo
- Pictures
- Click to enlarge.
-


Verification was done using two separate computers. Both of these computers had other tasks and were not dedicated to the computation.
All work for the verification was done entirely using spare CPU time.
Click here for a full list of computers that contributed to this computation.
Software: y-cruncher - A Multi-Threaded Pi Program/Benchmark
Software for Computation:
The program that was used for the main computation is y-cruncher v0.5.4.9138 Alpha.
See main page: y-cruncher - A Multi-Threaded Pi Program
y-cruncher is a powerful multi-threaded program/benchmark that is becoming an increasingly popular tool within the computer enthusiast community. As of this writing, it also holds the world record for most digits computed for several other famous constants. (These include: e, Square Root of 2, Golden Ratio, Euler-Mascheroni Constant, Natural Log of 2, Apery's Constant, and Catalan's Constant.)
There are several aspects of y-cruncher that set it apart from most other similar Pi-crunching programs:
- It uses state-of-the-art algorithms to achieve never-before-seen computational speeds. Many of these methods and algorithms are newly developed and first-time tested in y-cruncher. Therefore they are not yet used by other programs.
- y-cruncher is scalable to many cores. Most other multi-threaded Pi programs do not scale well beyond several cores and are unable to fully utilize many core machines such as the 12-core/24-thread computer that was used for this Pi computation.
- y-cruncher supports the use of multiple hard drives to use as distributed memory storage for very large computations.
- y-cruncher is fault-tolerant to hardware errors. It is able to detect and recover from minor computational errors that are caused by hardware anomalies or instablity. This is important for extremely long computations where the chance of hardware failure is non-negligible.
The exact version that was used for the computation is:
y-cruncher v0.5.4.9138 Alpha (PB) - x64 SSE4.1 ~ Ushio
This version was a very early private-beta for v0.5.4. It was slightly modified to display more detail on the progress of the computation. (All public versions display only a percentage.)
Software for Verification:
The program that was used for the verification is y-cruncher BBP v1.0.119.
See main page: y-cruncher BBP
This program implements the digit-extraction algorithm for Pi using the BBP formulas. It's sole purpose was to verify the main computation.
Both programs are written by me (Alexander J. Yee) and are available for download from their respective pages.
For those who have used y-cruncher before and are curious at how it works:
This webpage is the first article I have written that reveals significant details on the inner workings of y-cruncher... Enjoy!
Although the main computation was done on one computer. There were other computers that were involved. Below is a complete list detailing all the computers that contributed to this computation.
| Computer / Location | Owner | Main Specifications | Internal Storage Specifications | Task |
| Main (Japan) |
Shigeru Kondo | Prior to May 1: Processor: 2 x Intel Xeon X5650 @ 2.66 GHz Memory: 96 GB - DDR3 ECC @ 1066 MHz Motherboard: ASUS Z8PE-D18 OS: Windows Server 2008 R2 Enterprise x64
After May 1: (for the main computation) Processor: 2 x Intel Xeon X5680 @ 3.33 GHz Memory: 96 GB - DDR3 ECC @ 1066 MHz Motherboard: ASUS Z8PE-D12 OS: Windows Server 2008 R2 Enterprise x64 |
Controller: 2 x LSI MegaRaid SAS 9260-8i 1 TB - Boot |
Perform the Main Computation |
| Ushio (Evanston, Illinois) |
Alexander Yee | Processor: Intel Core i7 920 @ 3.5 GHz (OC'ed) Memory: 12 GB - DDR3 @ 1333 MHz (OC'ed) Graphics: EVGA GeForce GTX 275 Motherboard: Asus Rampage II GENE OS: Windows 7 Ultimate x64 |
Prior to June 19: 1.5 TB Seagate - Boot
After June 19: (offline for the summer) 1.5 TB Seagate - Boot |
Run the BBP formulas to verify the main computation. |
| Nagisa (Foster City, California) |
Alexander Yee | Prior to March 19: Processor: 2 x Intel Xeon X5482 @ 3.2 GHz Memory: 64 GB - DDR2 FB-DIMM @ 800 MHz Graphics: XFX GeForce GTX 9800+ Motherboard: Tyan Tempest S5397 OS: Windows Vista Ultimate x64
After March 19: Processor: 2 x Intel Xeon X5482 @ 3.2 GHz Memory: 64 GB - DDR2 FB-DIMM @ 800 MHz Graphics: PNY GeForce GTS 250 Motherboard: Tyan Tempest S5397 OS: Windows 7 Ultimate x64 |
Prior to March 19: Controller: SuperMicro AOC-SAT2-MV8 64 GB SSD (G.SKILL) - Boot
Prior to June 22: Controller: SuperMicro AOC-SAT2-MV8 1.5 TB Seagate - Boot
After June 22: Controller: SuperMicro AOC-SAT2-MV8 1.5 TB Seagate - Boot
After July 8: Controller: SuperMicro AOC-SAT2-MV8 64 GB SSD (G.SKILL) - Boot 1.5 TB Seagate - Data |
24/7 standby to deal with any urgent problems that might arise during the main computation.
Throughout the computation, this computer was mainly used for other unrelated tasks.
The main contribution of this computer was during the development of y-cruncher. It contributed very little to the actual computation itself.
During development, this was by far the most important computer I had as it was the only machine in my possession that could test memory-intensive code. |
Note that there were at least 8 other computers that took part in the development and testing of y-cruncher. But aside from a couple of spectacular laptops, most of these other machines had less than impressive specs and are not worth mentioning. (nor did any of them take part in the actual computation)
For the main computation, the following formula was used:
Chudnovsky Formula:
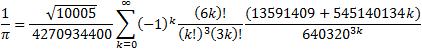
Verification was done using the following two BBP formulas:
Plouffe's Formula:
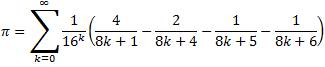
Bellard's Formula:
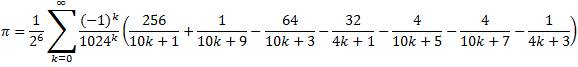
Chudnovsky's Formula was used with Binary Splitting to compute 4,152,410,118,610 hexadecimal digits of Pi. (+ about 40 safety digits)
To verify correctness of the hexadecimal digits, the BBP formulas were used to directly compute hexadecimal digits at various places (including the 4,152,410,118,610th place).
The two primary verification runs consisted of running both formulas to compute 32 hexadecimal digits ending with the 4,152,410,118,610th. These were done simultaneously on two different computers - "Ushio" and "Nagisa". Both computations were started at the same time.
The faster formula (Bellard) was assigned to the slower computer (Ushio) and the slower formula (Plouffe) was assigned to the faster computer (Nagisa).
As a result, both computations ended at roughly the same time (64 and 66 hours respectively).
Subsequent runs using the BBP formulas were done exclusively using "Ushio".
One radix conversion was done to convert the digits from base 16 to base 10. This produced 5,000,000,000,000 decimal digits. (+ about 50 safety digits)
The radix conversion was verified using modular hash checks. (see Sufficiency of Verification)
The method of verification is similar (if not identical) to the method that Fabrice Bellard used to verify his record of 2.7 trillion digits.
Unlike most world record-sized computation, only one main computation was performed. To provide sufficient redundancy to ensure that the computed digits are correct, several error-checking steps were added to the computation.
Verification of Hexadecimal Digits
As mentioned in the previous section, the hexadecimal digits were verified by directly computing the digits at various places and comparing them with the main computation. This combined with a Modular Hash Check on the final multiplication is sufficient to verify ALL the digits of the main computation.
We will start by listing a few assertions about high precision arithmetic.
Assertion #1: Last digits are correct -> All digits are correct
This assumption does NOT always hold. We will come back to this.
Assertion #2: Any error prior to a floating-point (N x N -> N digit) multiplication will propagate to the last digits of the product (after the multiplication).
This assertion is clearly true based on the nature of multiplication. The proof will be omitted.
Assertion #3: Any error DURING a multiplication will NOT always propagate to the last digits of the product (after the multiplication).
Depending on the where the error occurs, the last digits of a product may or may not be affected by an error occuring during the product.
(This is especially true if the error occurs in the inverse transform or the final carryout of an FFT-based multiply.)
The Reasoning:
- If Assertion #1 holds, then the BBP formula is sufficient as verification for ALL the digits.
- Chudnovsky's Formula ends with one final floating-point (N x N -> N digit) multiplication.
Based on Assertion #2, Assertion #1 will hold if there are no errors in the final multiply. - This leaves only one place for error. The final multiply itself. But this final multiply is verified using a Modular Hash Check.
- Therefore, any error in the computation will either have propagated to the last digits OR will fail the Modular Hash Check.
Verification of Decimal Digits
After the radix conversion, Pi is available in both base 16 and base 10.
Given that the base 16 digits are correct, the base 10 digits were verified as follows:
N = # of decimal digits desired (5,000,000,000,000 digits)
p = 64-bit prime number
![]()
![]()
![]()
Compute (using base 10 arithmetic):
![]()
Compute (using binary arithmetic):
![]()
If A = B, then with "extremely high probability", the conversion is correct.
"Extremely high probability" in this case means: If the conversion is incorrect, the probability that A = B is about 1 in ~264.
y-cruncher stores large integers as arrays of 32-bit integer-words in little-endian format.
Floating-Point numbers are stored as large integers with a sign and a 64-bit exponent.
Large numbers that reside on disk as stored the same way, but with a file handle instead of a pointer to memory.
All basic arithmetic uses 32-bit integer-words. 64-bit integers are used only for carry handling and indexing.
Since y-cruncher uses no assembly or inline assembly, the use of 64-bit words is not possible due the lack of a 128-bit integer type in C/C++ for carry handling.
Nevertheless, this is not a major drawback because y-cruncher actually spends very little time doing arithmetic in the integer unit. Most of the run-time is spent executing vector SSE and stalling on memory and disk access.
So for small computations, the bottleneck is the throughput of the SSE floating-point unit.
For large computations, the bottleneck is either memory bandwidth or disk bandwidth depending on the number of hard drives and their configuration.
Multiplication (All in Ram)
Small products are done using the Basecase and Karatsuba multiplication algorithms. 3-way Toom-Cook was also implemented, but it was effectively disabled by the optimizer because it is never optimal to use.
Medium-sized products are done using Floating-Point Fast Fourier Transform (Floating-Point FFT) convolution.
y-cruncher uses a modified FFT that is able to achieve Split-Radix computational complexity and numerical stability while maintaining the same friendly memory access pattern as the simple-radix algorithms.
FFT transform lengths of 2k, 3 * 2k, and 5 * 2k were used. Transform lengths of 7 * 2k were not used because they only benefit large products which are already handled by the Hybrid NTT algorithm below. It also unnecessarily increases the sizes of the Twiddle Factor tables.
The FFT is currently the most heavily optimized part of the program and uses vector SSE2, SSE3, and SSE4.1 instructions. Despite the lack of hand-coded assembly, the 64-bit version of the FFT achieves speeds comparable to that of prime95. (prime95 is known for having the fastest known FFT for x86 - much faster than FFTW)
Backward compatibility is maintained for processors that do not support SSE3 or SSE4.1. Future varients of the FFT will be able to utilize 256-bit AVX and FMA instructions.
Large products are done using Hybridized Number-Theoretic Transforms (Hybrid NTT).
The Hybrid NTT is a currently unpublished algorithm that was first conceived back in 2007 and then developed and implemented in 2008.
It is able to achieve speeds comparable to that of floating-point FFT while requiring only a fraction of the memory and memory bandwidth.
(The details of the Hybrid NTT will be left beyond the scope of this article.)
The current implementation used by y-cruncher is multi-threaded and uses both integer and floating-point instructions. This has a side bonus of gaining additional benefit from HyperThreading Technology. It supports SSE3, SSE4.1, and is expected to gain an additional speedup from AVX and FMA.
The multiplication algorithms described here have been present in y-cruncher since version v0.1.0 (the very first release). However, they have since had some fairly significant modifications. (The FFT was completely rewritten between v0.4.4 and v0.5.2. And the Hybrid NTT was re-tuned between v0.4.4 and 0.5.2.)
Multiplication (Disk)
Disk multiplications are the gigantic multiplications that will not fit in memory. These are done exclusively using Hybrid NTT.
When the ratio of (product size / memory2) is relatively small, a 3-step (or 3-pass) convolution algorithm is used.
- Pass 1:
- Read operand.
- Start the forward transform.
- Pass 2:
- Finish the forward transform.
- Perform point-wise multiplies.
- Start the inverse transform.
- Pass 3:
- Finish the inverse transform.
- Perform carryout.
- Write to destination.
This is the fastest known approach for performing a disk FFT that cannot be fit in memory.
When the ratio of (product size / memory2) is huge, disk seeks due to non-sequential disk access becomes a huge problem.
The solution is to use the 5-step (or 5-pass) convolution algorithm.
- Pass 1:
- Read operand.
- Start the forward transform.
- Pass 2:
- Do middle portion of the forward transform.
- Pass 3:
- Finish the forward transform.
- Perform point-wise multiplies.
- Start the inverse transform.
- Pass 4:
- Do middle portion of the inverse transform.
- Pass 5:
- Finish the inverse transform.
- Perform carryout.
- Write to destination.
The threshold at which the program will switch between 3-step and 5-step is a carefully tuned value based on the 2TB 7200RPM desktop hard drives that were available at the time when this part of the program that was written. 7-step (or more) can also be used, but is unnecessary with the amount of ram we had.
Because of the massive amount of ram that was available (96 GB), only the largest multiplications (2 trillion x 2 trillion digits or more) used the 5-step method.
In actuality, we had 144 GB of ram at our disposal (which is enough to completely eliminate the need for the 5-step method), but due to restrictions in hardware specifications, 144 GB of ram would have run at a lower clock speed. (96 GB ran at 1066 MHz, but 144 GB ran at 800 MHz.)
With respect to the size of our computation (5 trillion digits) and our hardware configuration (16 hard drives), it was found that 144 GB of ram is near the point of diminishing return for memory quantity. Therefore, additional memory clock speed provided more benefit than additional memory quantity. If we used only 48 GB of ram we could have run the memory at an even faster 1333 MHz. But 48 GB of ram was found to be less than optimal.
Running only 48 GB of ram would also allow us to use the EVGA SR-2 motherboard* which has overclocking capability. But the benefit of faster ram and CPU/memory overclockability was not worth the decrease in total ram as well as the potential risk for hardware instability - especially for such an extremely long running computation with low tolerance for hardware errors.
(Due to the memory intensive nature of the computation, the total amount of memory here is important - which seems to matter more than the speed of the CPU. Although 144 GB is at the point of dimishing return, 48 GB is the exact opposite. We estimate that clocking the CPU to 3.33 GHz with 96 GB of ram would probably run faster than clocking the CPU to 4+ GHz with only 48 GB of ram.)
*Note that at the time, it was believed that the EVGA SR-2 motherboard could only support up to 48 GB of ram. But it was found out later that, despite what EVGA officials stated, the motherboard is in fact capable of supporting up to 96 GB of ram.
The disk multiplication described here has been present in y-cruncher since v0.5.2 (the first version with Advanced Swap Mode).
Division + Square Roots
Divisions and Square Roots both use straight forward First-Order Newton's Method. No particular optimizations are done.
These are the least optimized parts of the program and there is plenty of room for improvement.
The following lists the major improvements that are NOT used:
- Middle Product extraction for the multiply-back step.
- Combine reciprocal and final multiply for division to reduce redundancy.
- Reuse redundant transforms for FFT-based multiplication.
The implementations for Division and Square Root that are used in y-cruncher have been virtually untouched since v0.1.0 (the first release).
Radix Conversion
The final radix conversion from base 16 to base 10 was done using Scaled Remainder Trees. This is the same algorithm that Fabrice Bellard used in his computation of 2.7 trillion digits. The only difference was that the Middle Product optimizations were not used.
The radix conversion is automatically verified at the end of each computation for two purposes.
- For world record attempts: Ensure correctness without the need for a second conversion.
- For competitive benchmarking: To catch that any computation errors that fail to propagate to the last digits.
This verification is done after the digits have already been written to disk. For benchmarks, it does not count towards computation time.
The Scaled Remainder Tree algorithm was added to y-cruncher in v0.5.3. Prior to v0.5.3, it used the classic Divide-and-Conquer algorithm.
The radix conversion verification was also added to y-cruncher in v0.5.3.
Given the amount of hardware that was used, scalability is one of the most important factors to performance. In this section, we discuss scalability in terms of both parallelism/multi-core as well as distributed memory/multi-hard drive.
Multi-Threading
With current trends in hardware heading to an ever-increasingly paralleled environment, the ability to scale effectively onto many cores is a major factor in performance.
And as such, y-cruncher makes extensive use of multi-threading.
- Binary Splitting - The Binary Splitting algorithm for series summation is trivially paralleled in that it recurses into independent work units.
In y-cruncher, this portion of the algorithm is paralleled using Binary Recursive Thread-Spawning. In Binary Recursive Thread-Spawning, each level of the recursion is called with a thread-limit that tells it how many threads it is allowed to use. Then each of the two recursive calls are called with exactly half of this thread-limit. When the recursive calls are complete, the merge is done using multi-threaded arithmetic. (using the full thread-limit)
Load-balancing issues aside, this method is asymptotically optimal in that CPU utilization approaches 100% as the number of digits increases.
- FFT-based Multiplication - As hinted from above, the multiplication is also multi-threaded.
Like with Binary Splitting, the Fast Fourier Transform (FFT) and related transforms are also trivially paralleled. In y-cruncher, they are also done using Binary Recursive Thread-Spawning in a virtually identical manner.
As with Binary Splitting, this method is asymptotically optimal. Due to the symmetrical structure of the FFT, there are no major load-balancing issues. Any minor load imbalance is usually caused by the environment as opposed the algorithm itself.
It should be noted that the Binary Recursive Thread-Spawning approach is the primary reason why y-cruncher restricts the # of threads to powers of two.
Multi-threading has been present in y-cruncher since the beginning (v0.1.0).
Multiple Hard Drive Support
Hard drives are one of the slowest things in modern computers. Moore's Law for disk bandwidth has not been keeping up with that of CPU computing power. And as such, disk bandwidth has fallen far behind the CPU. Given the memory-intensive nature of high precision arithmetic, performing arithmetic on disk is extremely bottlenecked by the speed of the disk. To combat this problem, y-cruncher supports the use of multiple hard drives to increase disk bandwidth.
The multiple hard drive feature in y-cruncher is essentially a software RAID 0. This may seem redundant of hardware RAID, but it provides 2 major advantages over hardware raid:
- The is no limit to the number of drives that can be used. Most hardware RAID controllers are limited to 4 or 6 drives. OS-supported software RAID can solve this problem, but is usually less efficient. For our computation, we used 16 hard drives for a combined sequential bandwidth of nearly 2 GB/s.
- By giving y-cruncher full control of each hard drive, it lets the program choose its own striping parameters (among other things).
- It allows the program to choose the stripe size and change it dynamically.
- It allows the program to choose between interleaved vs. append striping and change it dynamically.
This last point is important. Different operations are better suited to different RAID modes. For example, additions and subtractions require maximum linear speed and are therefore most efficient with interleaved striping. FFTs, on the other hand, do many non-sequential accesses and are most efficient with append striping since it allows simultaneous access to different parts of a file.
Multi-Hard Drive support has been present in y-cruncher since the beginning (v0.1.0).
However, prior to v0.5.2, it used only append striping. Starting from v0.5.2, it uses both append and interleaved striping.
Minimizing Bandwidth Consumption
Memory access patterns are one of the less obvious barriers to scalability. More cores and high CPU utilization means nothing if the software is bounded by another resource such as memory bandwidth.
For a memory-intensive program to scale well on many cores, it must have a high (computation work / bytes of memory access) ratio.
The problem is that all common operations in high-precision arithmetic have a very low value for this ratio. Addition and subtraction are the best examples of this since they do very little work, yet they need to pass over all the memory that holds the operands.
The bandwidth consumption of additions and subtractions is a relatively small problem because they only account for a very small portion of run-time. A much bigger problem is in the FFTs - which are notorious for their memory and bandwidth consumption.
From our experiments, a single large SSE-optimized radix-4 floating-point FFT is able to saturate the memory bandwidth on an Intel Core 2 Quad based system.
This means that attempting to multi-thread the FFT on this system will produce very little benefit since a single thread is already enough to hog all the memory bandwidth. Upgrading the hardware is only a partial solution. But even on the latest Intel Nehalem-based processors with 3 channels of DDR3, there is not enough bandwidth to keep the CPU fed when running 4 FFT threads - let alone 8 threads via HyperThreading.
To deal with this problem, a lot effort was put into minimizing memory access and improving the (computation work / bytes of memory access) ratio.
- Additions and subtractions are done in place whenever possible.
- Modular Hash Checks (described in the next section), are kept to a minimum.
- When Floating-Point FFTs are too large to fit into CPU cache (after being divided up among all the threads), Hybrid NTTs are used instead.*
*This last point is important. Due to complications involving cache associativity and insufficient registers, all attempts to make Floating-Point FFT efficient outside of CPU cache in the multi-threaded environment were scrapped. The decision was eventually made to use Hybrid NTT whenever Floating-Point FFT does not fit into cache. Although this increases computational cost, the reduced bandwidth consumption more than makes up for it.
Bandwidth-related optimizations have been in y-cruncher since the beginning (v0.1.0). But they have been improved and re-tuned numerous times since then.
The biggest improvement in the bandwidth-related optimizations was between v0.1.0 - v0.2.1, and v0.4.2 - v0.4.3.
Thread-Spamming and Load-Balancing
Due the asymmetrical nature of the series summation, parallelizing the Binary Splitting processes has significant load-balancing issues.
To deal with this, y-cruncher uses the following two methods:
Size-Balancing:
At each recursive level of binary splitting, the split is chosen carefully such that each sub-recursion will produce numbers of equal size.
This is in contrast to simply splitting the terms equally among the two sub-recursions.
In virtually all series summation, the earlier terms produce smaller numbers than later terms. (For example: Summing terms 1 - 100 produces a smaller result than summing terms 1,000,001 - 1,000,100 despite having the same # of terms.)
This method of size-balancing seeks to compensate for this discrepancy by giving more terms to the sub-recursion that sums up the earlier terms.
By balancing the sizes, it ensures a more balanced load between the threads. It also has a side-bonus of balancing memory usage among all the threads.
To do this, y-cruncher uses functional approximations to estimate the sizes of the numbers after summing up a range of terms.
These approximations (the details of which will be omitted) are able to estimate the sizes of each number in the recursion with an accuracy of about +/- one word-size from the actual sizes. (Even when the numbers are billions of word-sizes long.)
Thread-Spamming:
The size balancing method above is typically able to achieve a load-balance efficiency of about ~90%. (Meaning, one sub-recursion will rarely be more than 10% faster or slower than the other.)
But it is possible to do better than that. Here we apply a method which I call "Thread-Spamming".
Thread-Spamming does exactly what its name implies. It spams threads with the goal of increasing CPU utilization. At various places in the program, the number of allowed threads is doubled or even quadrupled depending on the known severity of the load-imbalance. Binary Splitting is one of these places.
The concept is very simple. By doubling the number of threads, each sub-recursion is capable of saturating all logical-cores by itself. This means that if one sub-recursion finishes before the other, the one that is still running will still be able to keep the processor busy. This ultimately increases CPU utilization.
The obvious problem is that too many threads can backfire due to threading overhead and resource contention. However, experiments have shown that the speed-up gained from utilizing those unused CPU cycles usually exceeds such overhead. (at least for shared memory and uniform memory environments...)
Both Size-Balancing and Thread-Spamming have been used by y-cruncher since the beginning (v0.1.0).
Error-Detection and Correction
For extremely long-running computations, it is necessary to consider the possibility of computation errors.
Even on stable and non-overclocked hardware, there is a non-negligible chance of a hardware error if it is put under stress for an extended period of time.
For better or worse, highly-optimized programs have a tendency to be extremely stressful to the hardware. y-cruncher is no exception. It is known to produce more heat than both Linpack and Prime95 on the Intel Nehalem-based processors when HyperThreading Technology is enabled. (Which is exactly what we used.)
(Linpack and Prime95 are very popular programs for stress-testing.)
So in some sense, the performance brought on by extreme optimization is a double-edged sword that must be dealt with. But of course, it is always better to avoid the errors in the first place, so extra care must be taken when building hardware that will run y-cruncher for extended periods of time.
Both Shigeru Kondo and myself have both experienced hardware related computational errors even on non-overclocked hardware. Between the two of us we get about one error for every 4 weeks of 100% CPU utilization (from y-cruncher) on our non-overclocked dual-socket machines. This comes to about 1 error for every 1017 operations. For a computation that would last much longer than that, there would be a significant chance of an error. And this was indeed the case.
At just a mere 8 days into the computation, a hardware error occured. Fortunately, the error-detection was able to catch the error. The error was unrecoverable so the computation was terminated and restarted from the previous checkpoint. The total time lost was about 1 day.
Had there been no error-detection, this error would have propagated to the final result and resulted in incorrect digits.
*Our observed error rate of 1 per 1017 operations seems unusually high for non-overclocked hardware. Whether it is coincidence, overheating, or simply an overly stressful load from y-cruncher, we have yet to find an explanation for this.
The error-detection and correction that y-cruncher uses is a simple "Automatic Repeat Request" model.
- Litter the entire program with redundancy checks.
- If an error is detected, repeat the operation that failed.
- If the operation cannot be repeated, then roll-back to the last save point.
Although several different methods of error-detection were used, only one was predominant - the Modular Hash Check.
Modular Hash Check
The Modular Hash Check is a very simple (and well-known) redundancy check that uses number-theory to verify the correctness of any operation that is closed under the modular-ring.
The operations we are interested in are:
![]()
![]()
![]()
To verify the correctness of a large integer addition, subtraction, or multiplication, simply take the modulus of both operands over a sufficiently large prime number p.
After the completing the operation, take the modulus of the result and apply the appropriate relation above. If it holds true, then with extremely high probability, the operation has been done correctly.
y-cruncher uses the mersenne prime, 261 - 1 as the chosen prime number for redundancy checking.
This ensures that an error will only have a 1 in 261 - 1 chance of passing the modular hash check. (Though this is somewhat arguable due to it being all 1-bits.)
This particular prime number was chosen solely for efficiency since computing a modulus over this prime needs only a few logical operations followed by an addition.
(Other primes at this size will require 64-bit divisions followed by multiply-back and subtract...)
This approach also works on floating-point numbers since the Modular Hash Check can be done prior to rounding or truncating.
In particular, the final multiply step in Chudnovsky's Formula for Pi used this method to verify its correctness.
Binary Splitting
Binary Splitting of the series accounts for over 80% of the total runtime in a Pi computation. Therefore, it is best place to place high-level redundancy checks.
The early stages of a binary splitting process involve no rounding and are comprised entirely of integer addition, subtraction, and multiplication. Modular Hash Checks were added to these places.
To minimize the performance penalty of these hash checks, the modular hash of each number is stored alongside the number. After each operation, the hash is updated using the relations above. (with negligible computation cost)
This avoids the need to check the hash after every single operation. Instead, the hash is only verified once (when the number is large enough to require swapping).
Once swapping begins, no more hash checking is done. This is because the Modular Hash Check requires a pass over each operand - which becomes extremely expensive when the binary splitting recursion is done on disk. At these sizes, the program relies on other internal checks. In any case, computation errors (not related to IO), are rare at the disk level because the CPU load is usually too low to generate the stress needed to cause computation errors.
Modular Hash Checks within Binary Splitting were added to y-cruncher in v0.5.3. Auto-recovery was added in the later builds of v0.5.4.
Radix Conversion
Based on the nature of the Scaled Remainder Tree algorithm for conversion, it is trivial to insert redundancy checks into (many places of) the algorithm with negligible computation overhead (the details of which will be omitted for conciseness).
As as result, the radix conversion is the most heavily error-checked portion of the entire program.
It should be noted that these error checks, although numerous, have yet to be proven sufficient for verification of the entire conversion. (It does not appear to be sufficient anyways...) Therefore, an extra step of Modular Hash Checks were added to the algorithm to ensure this.
Redundancy checking within the radix recursion was included with the first version (v0.5.3) that switched to the Scaled Remainder Tree algorithm. Auto-recovery was also included in v0.5.3.
Multiplication
Of the 4 multiplication algorithms that y-cruncher uses, only the Hybrid NTT has redundancy checks.
- Based on the nature of the Hybrid NTT (the details of which will be omitted for conciseness), it is possible to insert redundancy checks with negligible overhead.
- The Basecase and Karatsuba algorithms don't have any places to insert checks. The only way to check them is to use a full Modular Hash Check. (which is complete overkill if it is already covered by a higher level of error-detection)
- Floating-point FFT can be checked by examining the roundoff error, but that is less than trivial given the amount of optimization that has been done to it.
Fortunately, virtually all multiplications that are NOT done using Hybrid NTT are already covered by the Modular Hash Checks within the binary splitting step.
All swap multiplications use Hybrid NTT. This is the error-detection that the program relies on once the Modular Hash Checks within binary splitting are stopped.
Redundancy checking in the Hybrid NTT has been present in y-cruncher since the beginning (v0.1.0). Auto-recovery was also included in v0.1.0.
Some Random Comments
From reading multiple overclocking forums and from my own overclocking experiments, computation errors are usually caught by the Modular Hash Checks in binary splitting or by the checks within the Hybrid NTT. Rarely do errors manage to slip though the entire computation. (For v0.5.3, I have yet to see a single case where an error has made it through the entire computation without triggering any warnings or failing any redundancy checks.)
As of v0.5.3, the error-detection is not full-proof as there are still small parts of the program that inherently cannot be covered by redundancy checks. (or at least not without a significant performance cost) But it is sufficient as long as errors are not too common.
As a side note: The error-detection also guards against minor software bugs - which is a nice bonus.
Checkpointing + Restartability
Computation errors and hardware instability are one thing. But power outages are another. (among other things)
When running something that will take a hundred days, expect there to be problems, period.
To deal with this, y-cruncher has a checkpointing feature where it will save its progress. So that, if needed, it can restart from them.
This way, should the computation be stopped for whatever reason (power outage, computation error, magnitude 9.0 earthquake, or any sort of SimCity disaster, etc...), the computation can be restarted from a checkpoint (or savepoint).
Of course this relies on the swap disks being functional after the disaster, but this is easily fixed if backups of the swap disks are made periodically.
In Advanced Swap Mode, y-cruncher sets up checkpoints at various places in a computation. (Including multiple checkpoints within the series summation).
This ability to save and restart a computation is extremely important in that it nearly guarantees that a computation will eventually finish. Even in the case of a software bug that prevents the computation from finishing, the bug can be fixed and then restarted using the patched binary.
As with the error-detection, this feature came to the rescue at a mere 8 days into the computation.
Checkpointing was added to y-cruncher in v0.5.4. This was the final feature that was added prior to computing 5 trillion digits of Pi.
Despite being efficient enough to perform large computations, many of the algorithms and implementations in y-cruncher have plenty of room for improvment.
Sub-optimal Cache Use for Large Computations
Having been written and tuned for small computations that fit in ram, y-cruncher is sub-optimal for extremely large computations.
Most notably, the y-cruncher has a major problem with memory-thrashing for extremely large computations.
Due to time constraints, most of the algorithms that are used for disk operations had been "forcibly ported" from the in-ram equivalents with little or no regard to performance implications. Most of these performance penalties come in the form of sub-optimal cache use.
This sub-optimal cache use leads to excessive memory-thrashing which explains why Shigeru Kondo noticed that 96 GB of ram @ 1066 MHz had higher performance than 144 GB of ram @ 800 MHz.
Instruction Set Improvements
Large portions of y-cruncher do not fully utilize the SSE instructions that are supported by virtually all up-to-date x86/x64 processors.
Due to data-dependencies and alignment constrants, not everything can be easily vectorized. Although much of the code can be vectorized, they are not because they would require major changes to the program.
Mathematical Improvements
There are number of major optimizations that y-cruncher currently does not use. (And therefore were not used for this computation.)
- Middle Product - This optimization drastically speeds up Radix Conversions and the majority Newton's Method iterations. (Including Division and Square Root.)
This optimization was used extensively by Fabrice Bellard in the previous world record. - GCD Factorization - This optimization drastically speeds up the summation of the series. This was also used by Fabrice Bellard in the previous world record.
- Reuse Redundant Transforms for FFT-based Multiplication - This optimization attempts to eliminate redundant FFTs for multiplications where an operand is used more than once. This is a tricky optimization that is not widely used because it is highly situational and requires breaking through several layers of design encapsulation. Also, the benefit is marginal and rarely exceeds 17% overall speedup. (17% corresponds to 1/6 which is the maximum theoretical speed up this optimization will give in a lot of Binary Splitting recursions - including Pi.)
Algorithmic Improvements
There are a number of algorithms and design considerations that may or may not provide any benefit (for speed and memory).
None of these are implemented and are just sitting around in my scrapbook of ideas.
- Classic Number-Theoretic Transform over multiple primes - This is a very popular algorithm. It is used by PiFast, QuickPi, and Fabrice Bellard's TachusPi.
For a fixed word-size and a fixed number of primes, classic NTT has a perfect O(n log(n)) runtime complexity. This makes it asymptotically superior to the Hybrid NTT.
Since classic NTT uses integer divisions, it is notorious for being very slow. For that reason, its use is usually restricted to disk and low-memory environments.
However, it may be possible to make classic NTT efficient with careful use of Invarient Multiplication or Montgomery Reduction.
Currently, it is unknown whether classic NTT will be able to outperform the Hybrid NTT.
- Carry-Delay - With modern processors becoming more and more vectorized, a major barrier to improvement are the dependencies caused by carryout in multi-precision arithmetic. By using less than full-sized words, it is possible to break these dependency chains by delaying carryout. This allows for vectorization at the cost of increased memory consumption.
Carry-Delay will greatly benefit the lower-end algorithms such as Basecase and Karatsuba multiplication. However, they will not help FFTs and Hybrid NTTs because they do not have much in the way of carry-chains. Furthmore, FFTs and Hybrid NTTs dominate the total computation cost. Therefore, carry-delay is not expected to provide a huge overall benefit.
- Hybridized Number-Theoretic Transform (version 2) - This is an improved version of the Hybrid NTT that y-cruncher currently uses.
In more correct terms, this is a hypothetical implementation of the full Hybrid NTT algorithm that was developed back in 2008.
The Hybrid NTT that y-cruncher currently uses is merely a highly simplified version of the full algorithm that is much shorter and easier to implement.
The full Hybrid NTT has several theoretical advantages over the existing Hybrid NTT. However, it is extremely complicated. A fully optimized implementation that supports SSE4.1 and AVX instructions is estimated to require more than 100,000 lines of code.
Due to its extreme complexity, plans to implement the full Hybrid NTT in 2008 were completely scrapped in favor of the simplified version that is currently used by y-cruncher. Furthermore, the proof of correctness for the full algorithm was incomplete at the time. So it wasn't certain that the full algorithm would even work... (The proof has since been completed thanks to some help from Colleen Lee*.)
Feasibly speaking, efficiently implementing the full Hybrid NTT algorithm is out of reach. The sheer complexity of the algorithm combined with the lack of testable sub-steps makes it a very formidable task in front of which I stand helpless after multiple attempts.
So for now, the full Hybridized Number-Theoretic Transform will remain only of academic interest.
*Colleen Lee is one of my best friends from high school. As of this writing, she is an undergraduate at Stanford University.
Detailed Timeline (With Screenshots)
The computers here are referenced by their names. See the list of computers for what their specifications are.
| Date | Person / Computer | Event | Screenshot |
| Sometime in February | - | Following my announcement of 500 billion digits of e, Shigeru Kondo contacts me saying that he wishes to attempt 5 trillion digits of Pi. |
|
| March - April | - | I add lots of new developments and improvements to the program in preparation for such a large computation. During this time, Shigeru Kondo helped me do a lot of testing on these new features. |
|
| May 1, 2010 | Shigeru Kondo / Main | Shigeru Kondo finishes a computation of 1 trillion digits of Pi. Total Time: 13 days This was the final test and Kondo notifies me that he will attempt 5 trillion digits next. |
View |
| May 2, 2010 | Me / Ushio | Begin Computation: 32 hexadecimal digits ending with the 4,152,410,118,610th. |
|
| May 2, 2010 | Me / Nagisa | Begin Computation: 32 hexadecimal digits ending with the 4,152,410,118,610th. |
|
| May 4, 2010 | Shigeru Kondo / Main | Begin Computation: 5,000,000,000,000 digits of Pi. |
View |
| May 5, 2010 | Me / Ushio | Completed Computation: 32 hexadecimal digits ending with the 4,152,410,118,610th. |
View |
| May 5, 2010 | Me / Nagisa | Completed Computation: 32 hexadecimal digits ending with the 4,152,410,118,610th. |
View |
| May 7, 2010 | Me / Ushio | Begin Computation: 50 hexadecimal digits ending with the 2,000,000,000,000th. |
|
| May 9, 2010 | Me / Ushio | Completed Computation: 50 hexadecimal digits ending with the 2,000,000,000,000th. |
View |
| May 11, 2010 | Shigeru Kondo / Main | Week 1 Progress Update: Series summing is past 13% complete. |
View |
| May 12, 2010 | Shigeru Kondo / Main | Computation Error: The program's internal error-detection detects a computation error. |
View |
| May 12, 2010 | Me / Nagisa | I attempt reproduce the error on my own machine. But no error is detected. |
|
| May 13, 2010 | Shigeru Kondo / Main | Computation Error Update: The program passes the part of the computation error. Total time lost: ~ 1 day |
View |
| May 13, 2010 | Me / Ushio | Begin Computation: 50 hexadecimal digits ending with the 4,000,000,000,000th. |
|
| May 16, 2010 | Me / Ushio | Completed Computation: 50 hexadecimal digits ending with the 4,000,000,000,000th. |
View |
| May 16, 2010 | Me / Ushio | Begin Computation: 50 hexadecimal digits ending with the 4,000,000,000,000th. |
|
| May 18, 2010 | Shigeru Kondo / Main | Week 2 Progress Update: Series summing is past 22% complete. |
View |
| May 20, 2010 | Me / Ushio | Completed Computation: 50 hexadecimal digits ending with the 4,000,000,000,000th. |
View |
| May 20, 2010 | Me / Ushio | Begin Computation: 50 hexadecimal digits ending with the 3,000,000,000,000th. |
|
| May 22, 2010 | Me / Ushio | Completed Computation: 50 hexadecimal digits ending with the 3,000,000,000,000th. |
View |
| May 22, 2010 | Me / Ushio | Begin Computation: 50 hexadecimal digits ending with the 3,000,000,000,000th. |
|
| May 25, 2010 | Me / Ushio | Completed Computation: 50 hexadecimal digits ending with the 3,000,000,000,000th. |
View |
| May 26, 2010 | Shigeru Kondo / Main | Week 3 Progress Update: Series summing is past 36% complete. |
View |
| May 31, 2010 | Shigeru Kondo / Main | Week 4 Progress Update: Series summing is past 46% complete. |
|
| June 8, 2010 | Shigeru Kondo / Main | Week 5 Progress Update: Series summing is still somewhere past 46% complete. |
View |
| June 16, 2010 | Shigeru Kondo / Main | Week 6 Progress Update: Series summing is past 59% complete. |
View |
| June 22, 2010 | Shigeru Kondo / Main | Week 7 Progress Update: Series summing is still somewhere past 59% complete. |
View |
| June 29, 2010 | Shigeru Kondo / Main | Week 8 Progress Update: Series summing is past 76% complete. |
View |
| July 7, 2010 | Shigeru Kondo / Main | Week 9 Progress Update: Series summing is still somewhere past 76% complete. |
View |
| July 11, 2010 | Shigeru Kondo / Main | Day 68: Series summing is complete. Begin Division. |
View |
| July 16, 2010 | Shigeru Kondo / Main | Day 73: Performing the multiplication step of the division. |
View |
| July 19, 2010 | Shigeru Kondo / Main | Week 11 Progress Update: Performing Final Multiplication. |
View |
| July 22, 2010 | Shigeru Kondo / Main | Day 80: Pi computation is complete. Hexadecimal digits agree with BBP results!!! |
View |
| July 28, 2010 | Shigeru Kondo / Main | Week 12 Progress Update: Base Conversion is about 75% complete. |
View |
| August 1, 2010 | Shigeru Kondo / Main | Day 89: Base Conversion is complete. Results match the previous world record!!! |
View |
| August 2, 2010 | Shigeru Kondo / Main | Day 90: Verification of Base Conversion is complete. The new world record is 5 trillion digits!!! |
View |
These aren't restricted to this article. They include some random things I've been asked a lot in the past.
The homepage for y-cruncher has an FAQ for questions related to the software itself.
Question: Are you a mathematician?
Answer: No.
Question: Do you consider yourself good at math?
Answer: Not really... But I don't consider myself bad at it either.
Question: What will you be doing after you graduate from college?
Answer: I'll be going to the University of Illinois Urbana-Champaign for graduate school. After that, I don't know...
Question: What video games do you play?
Answer: I play mostly First Person Shooters (FPS) and Real-Time Strategy (RTS). Specific games include: Left 4 Dead, Team Fortress, Halo, Crysis, Starcraft, Warcraft DOTA, Age of Empires, and a bunch of older games. (Though I'm a lot better at FPS than RTS...)
Question: Why don't you use the GPU? They are much more powerful and cheaper than high-end CPUs.
Answer:
- GPUs have very poor double-precision support. Double-precision is required.
- The computation is almost entirely memory bound. It is not very limited by CPU. So the power of a GPU would largely be wasted.
- GPUs require massive vectorization to be efficient. Currently, y-cruncher is not scalable to large SIMD vectors.
- GPUs don't have enough memory. The bandwidth between GPU memory and main memory is far from sufficient to efficiently use main memory in place of GPU memory.
- There is no common standard for GP-GPU programming.
Question: Some of the higher-end video cards have a LOT of memory. The Nvidia Fermi-based Quadro cards have a whopping 6GB of ram. Why can't you use those?
Answer: Expensive would probably be an understatement... And for large swap computations, 6GB of ram would be a sure bottleneck. Something like 64GB or 128GB would more useful, but I don't see that happening anytime soon - let alone at an affordable price...
Question: You mention that you can't use GPU because of poor double-precision support. Why can't you use single-precision?
Answer: Because some of the algorithms used by y-cruncher will fail if there isn't enough precision. To some extent, single-precision can be forced, but the penalty in performance and memory will be obscene.
Question: Does y-cruncher use make any use of GMP or other open-sourced software? In other words, did you write the entire program by yourself?
Answer: Although there has been some influence from GMP and other sources, y-cruncher does not share any source code with anything else.
All the source code for y-cruncher and all its underlying libraries are entirely written by myself.
I would like to give a special thanks to all my friends and family who cheered me on during these 3 long months.
In particular, I would like to give a special thanks to Kei Simmel who served as our translator to help us manage our language barrier. I don't speak any Japanese, and Shigeru Kondo doesn't speak much English... Whenever google-translate failed miserably, Kei was there to help.
And lastly, is of course Shigeru Kondo himself. Without his help, this computation would not have been possible since I lacked the patience and resources to run this computation.
I'm a 22 year old senior-undergraduate student at Northwestern University. I actually graduated in June (which was during this 3-month long computation).
So technically speaking, I am no longer an undergraduate. However, I will be starting graduate school at the University of Illinois Urbana-Champaign in August.
I have a double major in Computer Science and Electrical Engineering. My concentrations are High Performance Computing, Parallel/Distributed Computing, and VLSI.
However, most of my knowledge in HPC and Parallel Computing are self-taught.
I grew up in Foster City, California and attended Bowditch Middle School.
After graduation, I moved to Palo Alto, CA where I attended and graduated from Palo Alto High School.
My hobbies include Bowling, Piano (music in general), Video Games, and subtitled Japanese Anime (i.e. I don't watch dubs...).
I speak English, Cantonese, and a tiny bit of Mandarin.
More about me.
Contact me via e-mail. I'm pretty good with responding unless it gets caught in my school's junk mail filter.
You can also find me on XtremeSystems Forums under the username: poke349
Back To: