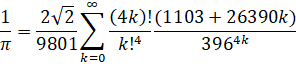User Guides - Custom Formulas
By Alexander Yee
(Last updated: January 31, 2024)
y-cruncher has always focused on a small number of constants so that they can be specialized and taken to the extreme. But for the first time ever, the project will break from that focus in an attempt to broaden its scope in a manner that minimally affects its original focus.
y-cruncher v0.7.7 adds a new experimental feature that will allow the user to specify a custom formula with which to evaluate. This finally allows y-cruncher to compute a much larger set of numbers beyond the built-in constants.
The custom formula feature is analogous to PiFast's "User Constants".
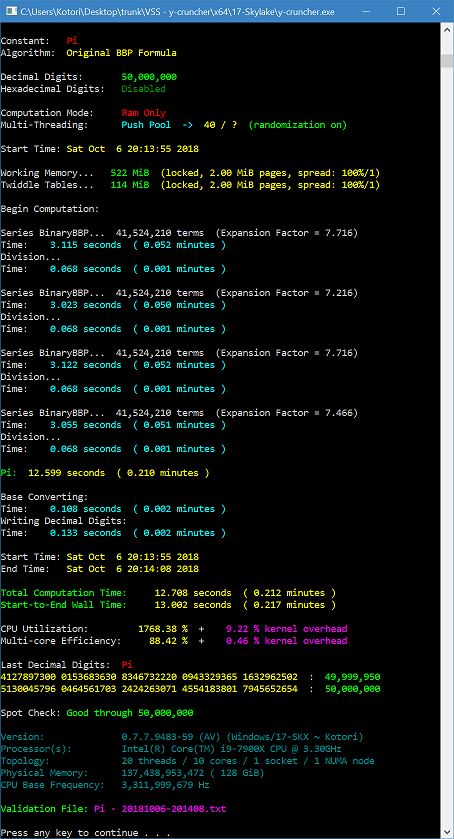
Computation of Pi using a Custom Formula
|
Usage:
Custom formulas are stored as ".cfg" files. These are essentially y-cruncher's configuration file format. The "Custom Formulas" folder in the y-cruncher folder will have a set of sample formulas that are ready to be fed into y-cruncher.
Entering a formula can be done in multiple ways:
- Using the console UI, it is option 10 in the constants menu. Then you need to specify the filename. The ".cfg" extension can be omitted.
- From the command line, it can be accessed in the Custom Compute option as another constant:
y-cruncher custom custom:"filename" [other options]
When entering a filename, you can omit the "Custom Formulas/" base path. y-cruncher will automatically search for it there.
Formula and Format:
The following example implements Ramanujan's formula for Pi:
{
NameShort : "Pi"
NameLong : "Pi"
AlgorithmShort : "Ramanujan"
AlgorithmLong : "Ramanujan (1910)"
Formula : {
Multiply : [
{
SeriesHypergeometric : {
Power : -1
CoefficientP : 1
CoefficientQ : 1103
CoefficientD : 9801
PolynomialP : [-3309 -54904 527636 -1231424 844480]
PolynomialQ : [0 0 0 3073907232]
PolynomialR : [-3 22 -48 32]
}
}
{Invsqrt : 8}
]
}
}
Many more examples can be found in the GitHub repo. Feel free to contribute more.
The use of the configuration file format to represent formulas is admittedly an abuse of the format. So it is somewhat clumsy and user-unfriendly to work with. Therefore, it is strongly recommended to build and test your formulas in an actual CAS (computer algebra system) before you plug it into y-cruncher.
The structure of a formula can be best described as a tree of nodes where each node is a function that takes its branches as inputs and returns a single value which is then passed up to the parent node. So it is (with one notable exception) a purely functional language. This representation closely resembles how the tree is executed internally by y-cruncher.
The root node consists of 5 fields:
- NameShort: The short version of the name of the constant. This will be used in the output file. So it cannot have characters that are illegal in filenames.
- NameLong: The long version of the name. This is for display inside y-cruncher.
- AlgorithmShort: Similar to NameShort. It is used in the output file name so it cannot have illegal filename characters.
- AlgorithmLong: Same idea as NameLong. Used only for display inside y-cruncher.
- Formula: The formula itself.
The meaning of the different object types (integer, string, array, object) is context-dependent. It is recommended to browse the examples before writing your own formula. The overall layout and syntax should be fairly easy to pick up.
When an enclosing function expects a large number, it can be one the following object types:
- An integer in the range: [2-63, 263)
- A bracket "{}" object with a single key/value pair where:
- The key is the function name.
- The value is the parameter(s) to the function.
- A string where the text is a variable that was defined earlier.
If it's an integer, it is promoted (upcast) to a large number. Some functions will recognize the integer and use a faster implementation for the integer.
If it's a bracket "{}" object, it is a function call.
If it's a string, it loads the variable named in the string. If the variable doesn't exist, y-cruncher will reject the formula.
There is no support for conditionals, loops, recursion, or user-defined functions. The custom formula format is not meant to be a programming language. The fixed structure of the tree is also how y-cruncher is able to pre-determine the resource requirements for a computation.
Precision:
All operations and all arithmetic are done at the full precision. There is currently no support for precision micromanagement.
Internally, y-cruncher does all calculations out to an additional 150 - 200 digits of precision. 100 of those digits are used to generate the "next-100" hash that goes in the validation file. The remaining 50 - 100 digits of precision are the guard digits.
For most formulas, this 50 - 100 guard digits will be sufficient to hide any round-off error. But it will not protect against inherent loss of precision or numerical instability such as destructive cancellation. Just because y-cruncher can do computations to extremely high precision doesn't make it immune to the usual effects of numerics.
Numerical Consistency:
y-cruncher isn't particularly fancy when it comes to handling numerical round off. The attitude has always been to "throw more precision at it". Because if you're already running at a billion digits, throwing in a couple hundred more isn't going to noticeably hurt performance.
As a result of the above:
- y-cruncher does not adhere to any floating-point specification. It only guarantees that all operations are carried out to at least the specified precision.
- y-cruncher makes no attempt to achieve numerical consistency against anything except for thread scheduling*.
The 2nd one means that you may get slightly different results depending on stuff like the computation mode (Ram vs. Swap). In most cases, this won't matter because these differences are small and will not propagate out of the 50 - 100 guard digits. But it is quite easy to artificially construct formulas that do.
For example, computing log(e) can yield either 1.000000... or 0.999999... This example abuses the fact that y-cruncher doesn't do consistent rounding. Then it uses the carryout edge case to bring the difference out of the guard digits to where it can be seen. Larger differences can be achieved using numerically unstable formulas.
External factors that are known to affect the numerical behavior are:
- The computation mode: Ram Only vs. Swap Mode
- In Swap Mode, the amount of memory that is being used.
- The task decomposition. (the amount of parallelism)
*Consistency aganst thread scheduling is something that y-cruncher has always maintained for the purpose of debuggability.
Computational Complexities:
Run-time and memory complexities are given for each operation where:
- n is the working precision
- M(n) is the cost of a large multiply. This is given for operations that have simple and well understood Big-O constants relative to large multiplication.
As of this writing, y-cruncher only supports functionality that satisfies all of the following:
- Quasi-linear or better run-time complexity.
- Linear or better memory complexity.
Since y-cruncher only accepts finite-sized formulas with no looping, every formula that it accepts will also meet the above criteria.
However, some functions (such as the AGM) have very large big-O constants and others (like SeriesHypergeometric) have input-dependent Big-O constants that can be unboundedly large.
There are some significant limitations in the custom formula feature. Many of these can be very inconvenient and are largely a reflection of how focused the program has historically been on a small set of very specific tasks.
Output Restrictions
Due to limitations in y-cruncher's radix conversion and digit output, y-cruncher can only output numbers that are positive with a magnitude near 1.0. Specifically, the number must be in the range:
- 32-bit Binary: output ∈ [2-32, 232)
- 64-bit Binary: output ∈ [2-64, 264)
y-cruncher will error out if the computed number falls outside of this range.
No Optimizations
y-cruncher is not a compiler nor is the configuration format meant to be a programming language. So no forms of optimization will be performed:
- No common subexpression elimination.
- No algebraic optimizations. (i.e. factoring)
- No elimination of useless computation. (i.e. multiply by zero)
In other words, what you write is what you get. So you need to do these optimizations yourself.
No Loops or Recursion
There is no support for loops or recursion. The formula must be fully inlined and thus finite in size. This has the side-effect of guaranteeing quasi-linear run-time and linear memory for all formulas that y-cruncher accepts.
No Dependencies
There is no support for external dependencies. The formula is therefore static and fully self-contained.
- You cannot reference another formula from elsewhere.
- You cannot load digits from a previous computation.
There is also no way to make the formula dependent on the working precision or the number of digits that's being computed. This unfortunately makes it impossible to implement a lot of approximation algorithms without hard-coding them to a specific precision.
Things that fall in this category are:
- Implementing your own log(x) using the AGM. This requires scaling that depends on the precision. Fortunately, y-cruncher provides this function.
- All known (fast) algorithms for the Euler-Mascheroni Constant*. All of them are approximation algorithms that change depending on the precision.
- Gamma function of a rational number by means of approximation from the lower incomplete gamma function evaluated at a large argument.
*This is just one of several reasons why you cannot implement the Euler-Mascheroni Constant without calling the built-in function for it.
Main Page: Functions List
As mentioned in an earlier section, the functional-language-like nature of the syntax maps to an execution tree that is built internally by y-cruncher. This tree is part of the "computation plan" that is built prior to a computation which dictates how the computation is done including where the data is laid out in memory.
This "computation plan" is what allows y-cruncher to pre-determine how much memory/storage is needed for a computation. Every function (node in the tree) has known constraints on its resource usage and where it writes its outputs. Thus y-cruncher can recursively walk the entire tree and simulate the computation to calculate the resource requirements for the entire computation.
At this time, there are no immediate plans to build an expression evaluator. In theory, all that's needed is a parser which compiles to either the current config format or directly into the internal execution tree. But y-cruncher was never intended to be a math research program and it's expected that everything should first be built using a CAS, then converted to a y-cruncher custom formula.