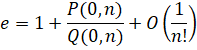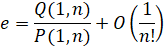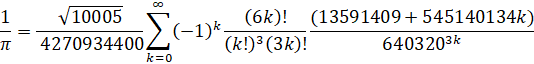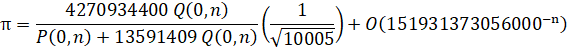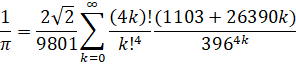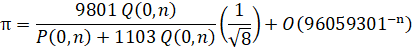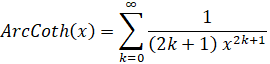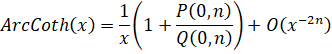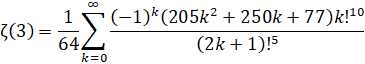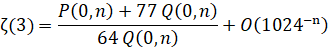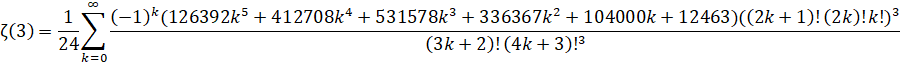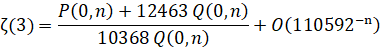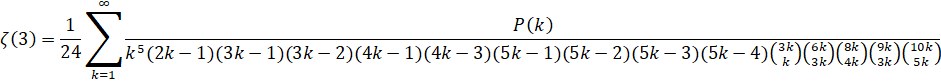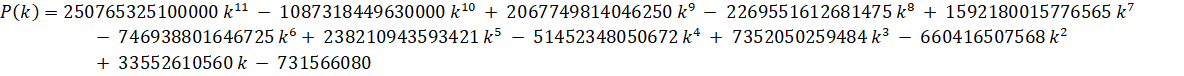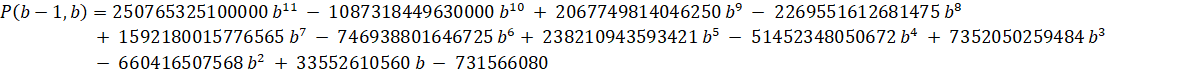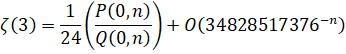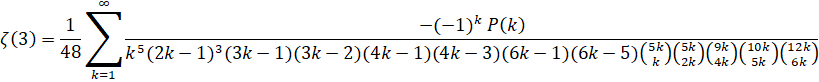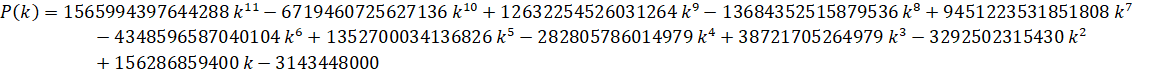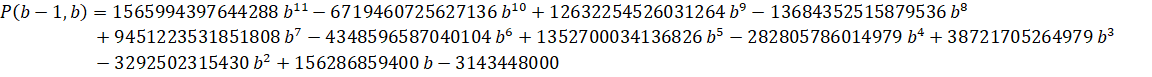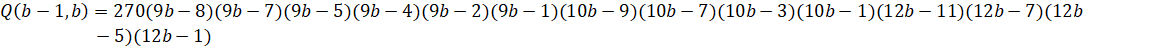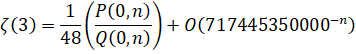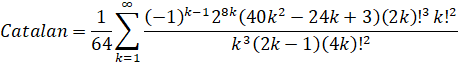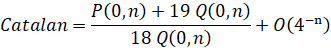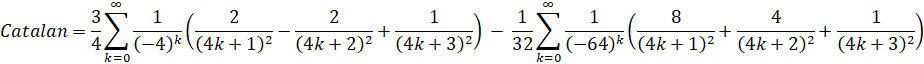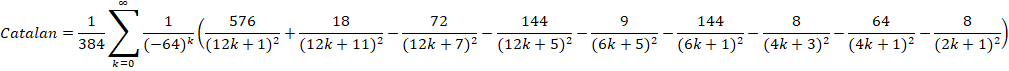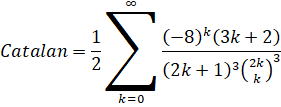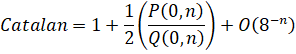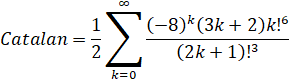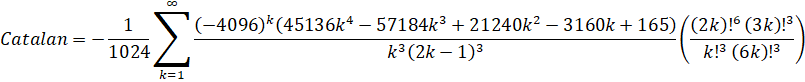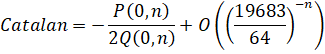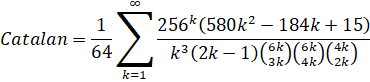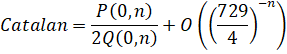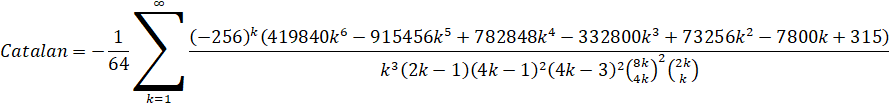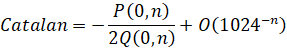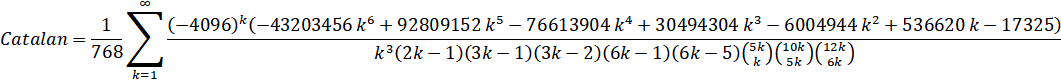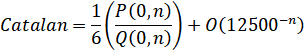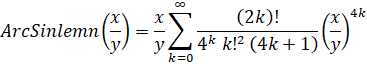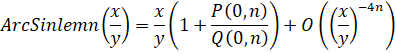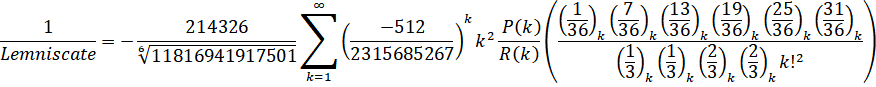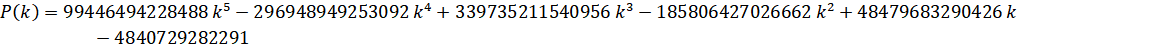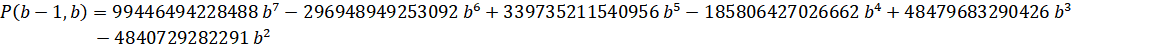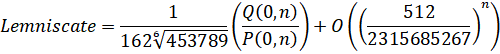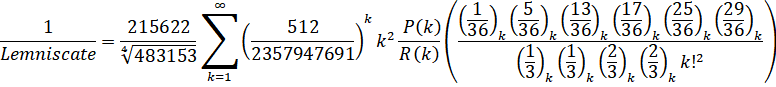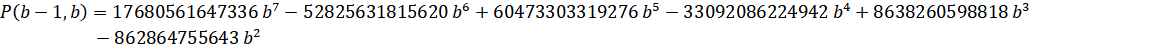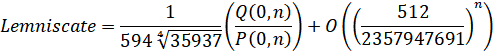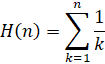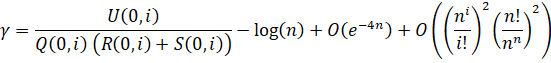Binary Splitting Recursion Library

By Alexander Yee

 

(Last updated: May 23, 2024)

 

 

 

Back To:

• Numberworld Home
• y-cruncher Home
• Algorithms and Internals

 

This is a dump of Binary Splitting recursions for various series and constants. For the most part, these are what y-cruncher uses.

All run-time complexities shown assume that large multiplication is O( N log(N) ).

 

 

Index:

• e:
  • exp(1)
  • exp(-1)


• Pi:
  • Chudnovsky (1989)
  • Ramanujan (1910)


• ArcCoth(x):
  • Taylor Series


• Zeta(3) - Apery's Constant:
  • Amdeberhan-Zeilberger (1997)
  • Wedeniwski (1998)
  • Zuniga (2023-v)
  • Zuniga (2023-vi)


• Catalan's Constant:
  • Lupas (2000)
  • Huvent (2006)
  • Guillera (2008)
  • Guillera (2019)
  • Pilehrood (2010-short)
  • Pilehrood (2010-long)
  • Zuniga (2023)


• Lemniscate:
  • Zuniga (2023-vii)
  • Zuniga (2023-viii)


• ArcSinlemn(x/y):
  • Series


• Euler-Mascheroni Constant:
  • Brent-McMillan (1980) Series A and B

 

---

e - exp(1):

 

Run-Time Complexity for N digits: O( N log(N)² )

 

Series Type: Hyperdescent

Series Speed: Superlinear

 

 

 

 

 

Custom Formula File: e - exp(1).cfg

 

---

e - exp(-1):

 

Run-Time Complexity for N digits: O( N log(N)² )

 

Series Type: Hyperdescent

Series Speed: Superlinear

 

 

 

 

 

Custom Formula File: e - exp(-1).cfg

 

---

Pi - Chudnovsky (1988):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 0.367)

 

 

 

 

 

Custom Formula File: Pi - Chudnovsky.cfg

 

---

Pi - Ramanujan (1910):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 0.653)

 

 

 

 

 

Custom Formula File: Pi - Ramanujan.cfg

 

---

ArcCoth(x) - Taylor Series:

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 4 / log(x²))

 

 

 

 

---

Zeta(3) - Amdeberhan-Zeilberger (1997):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 2.885)

 

 

 

 

 

Custom Formula File: Zeta(3) - Amdeberhan-Zeilberger.cfg

 

---

Zeta(3) - Wedeniwski (1998):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 2.755)

 

 

 

 

 

Custom Formula File: Zeta(3) - Wedeniwski.cfg

 

---

Zeta(3) - Zuniga (2023-v):

 

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 2.307)

 

 

 

 

 

Custom Formula File: Zeta(3) - Zuniga (2023-v).cfg

 

---

Zeta(3) - Zuniga (2023-vi):

 

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 2.051)

 

 

 

 

 

Custom Formula File: Zeta(3) - Zuniga (2023-vi).cfg

 

 

---

Catalan - Lupas (2000):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 11.542)

 

 

 

 

 

Custom Formula File: Catalan - Lupas.cfg

 

---

Catalan - Huvent (2006):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: BinaryBBP

Series Speed: Linearly Convergent (cost = 17.312)

 

 

Huvent's formula can be rearranged as follows:

 

 

Series Type: BinaryBBP

Series Speed: Linearly Convergent (cost = 12.984)

 

 

Custom Formula Files:

• Catalan - Huvent (original).cfg
• Catalan - Huvent (optimized).cfg

 

---

Catalan - Guillera (2008):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 11.542)

 

 

 

 

 

A trivial rearrangement of the formula leads to a much faster series:

 

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 5.771)

 

 

 

 

 

Custom Formula File: Catalan - Guillera (2008).cfg

 

---

Catalan - Guillera (2019):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 4.189)

 

 

 

 

 

Custom Formula File: Catalan - Guillera (2019).cfg

 

 

---

Catalan - Pilehrood (2010-short):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 3.074)

 

 

 

 

 

Custom Formula File: Catalan - Pilehrood (short).cfg

 

---

Catalan - Pilehrood (2010-long):

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 4.617)

 

 

 

 

 

Custom Formula File: Catalan - Pilehrood (long).cfg

 

---

Catalan - Zuniga (2023): (ETA: y-cruncher v0.8.3)

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 3.392)

 

 

 

 

 

Custom Formula File: Catalan - Zuniga (2023).cfg

 

---

ArcSinlemn(x/y) - Series:

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 2 / log(y/x))

 

 

 

 

---

Lemniscate - Zuniga (2023-vii):

 

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 1.566)

 

 

 

 

 

Custom Formula File: Lemniscate - Zuniga (2023-vii).cfg

 

---

Lemniscate - Zuniga (2023-viii):

 

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: CommonP2B3

Series Speed: Linearly Convergent (cost = 1.564)

 

 

 

 

 

Custom Formula File: Lemniscate - Zuniga (2023-viii).cfg

 

---

Euler-Mascheroni Constant - Brent-McMillan (1980) Series A and B:

The Brent-McMillan formula is an approximation to the Euler-Mascheroni Constant.

 

                

 

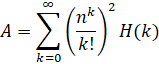
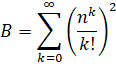
The parameter n determines how good the approximation is. To compute N digits, you must pick a suitably large n such that the approximation is sufficient.

 

Run-Time Complexity for N digits: O( N log(N)³ )

 

Series Type: Specialized

Series Speed: Superlinear for a fixed n

 

 

 

 

Note that there are two error bounds in this final formula:

• The 1st one, O(e^-4n) is from the series being an approximation rather than an equality.
• The 2nd one is from the number of terms that have been summed up.

The series is divergent for the first n terms. The 2nd error bound only holds when the series begins converging. Therefore you must sum at least n terms.

 

If n has been chosen carefully to reach exactly the desired precision, then the number of terms i to be summed should be chosen such that the second error bound reaches the same desired precision. This can be done by setting i as follows:

 

 

where the 3.59112... is the solution to the following equation:

 

 

 

This 7-variable recursion shown above is freshly derived and unoptimized. The one that y-cruncher uses is optimized down to 4 variables.

But to break it down a bit:

• P and Q are the harmonic numbers summed up using the BinaryBBP recursion with r = 0.
• R, S, and T is series B using the CommonP2B3 recursion.
• U and V, puts the two together to construct series A.

 

The Brent-McMillan formula is by far the most difficult and complicated to implement among the mainstream constants:

• The 7-variable Binary Splitting recursion is significantly more complicated and difficult to derive than most other recursions.
• The formula is an approximation which leads to multiple error-bounds that need to be dealt with.
• The initially divergent behavior followed by non-linear convergence can cause lead to difficulties not present with other (better behaved) algorithms.
• While not shown here, the refinement term is a divergent asympotic series with the opposite convergence behavior as the above.
• Hardly worth mentioning, but the formula does require an implementation of log(n).