The Hybrid NTT

By Alexander Yee

 

(Last updated: July 19, 2023)

 

 

Back To:

 

The Hybrid NTT (short for Hybridized Number-Theoretic Transform) is the algorithm that founded the y-cruncher project.

 

At the time it was conceived (2007), it was by far the most powerful large multiplication algorithm. While it was neither the fastest nor the most memory efficient, it had the unique trait of being both good enough at both to fully benefit from parallelism at the dawn of the multi-core era.

 

The Hybrid NTT remained the most important algorithm in y-cruncher from 2007 to about 2013 when it started getting overtaken by newer vectorizable algorithms that would better utilize the increasingly powerful SIMD on modern computers.

 

As of y-cruncher v0.8.1, the Hybrid NTT has been removed, thus marking the end of an era for y-cruncher.

 

 

Background

 

Back in 2008, the biggest problem in large multiplication was the "FFT vs. NTT" problem. This refers to the nasty space-time tradeoff between floating-point FFTs and integer NTTs.

 

Historically, there were (and still are) 3 classes of algorithms for large sizes that were used in practice:

All 3 algorithms run in approximately O(N*log(N)) time and are thus "fast". However, the Big-O constants (as of 2008) for both speed and memory are at opposite extremes of a space-time tradeoff with nothing in between where it was needed the most.

 

At one extreme, the Floating-Point FFT is the fastest - 10x faster than both NTT and SSA. But at the other extreme, the NTT and SSA (which are similar in performance) are ~4x more memory efficient. Thus (as of 2008), the only two points in the space-time tradeoff was choosing 10x performance at 4x the memory cost.

 

While the memory cost of 4x may seem inconsequential in most cases, Pi computation and other "extreme" bignum projects are intended to push the limits of hardware. Thus a 4x memory cost is generally unacceptable. Coincidentally, 2008 was also the dawn of the age of multi-core and parallel computing. And this was the also the time when memory bandwidth started becoming a bottleneck. FFTs, having 4x the memory cost would also imply 4x the bandwidth requirements.

 

So while FFTs are 10x faster on paper, this only applied to single-threaded computations. With parallelism, the speedup would often be capped to only ~2x because FFTs become limited by memory bandwidth very quickly. Thus FFTs simply didn't scale on multi-core systems. On the other side, NTT and SSA had the opposite problem. Being 10x slower and 4x more memory efficient, they were not memory-bound. But being 10x slower meant that even with parallelism, they still weren't going to outperform the floating-point FFT.

Algorithm Relative Computational Cost Relative Memory Requrements Relative Compute/Memory Ratio
Floating-Point FFT x86 + x64 1.0 4.0 0.25
32-bit Small Primes NTT x86 + x64 10.0 1.2 8.33
Schönhage-Strassen Algorithm (SSA) x86 10.0 1.0 10.00
x64 8.0 8.00

This table above shows the drastic difference in compute density of the FFT vs. the NTTs.
In 2008, most hardware had a compute/memory ratio of about ~2.0. Thus FFTs were heavily memory-bound while NTTs were heavily compute-bound.

 

To summarize:

  1. FFTs are 10x faster than NTTs and SSA. But it also uses 4x more memory and memory bandwidth.
  2. NTTs and SSA are 10x slower, but is 4x more memory efficient.
  3. FFTs are so memory-bound that they don't scale with parallelism.
  4. NTTs and SSA are so slow that even when parallelized, they cannot beat FFTs.

For a 2008-era 8-core server (2 x Xeon X5482), parallelizing across all 8 cores could not bring more than about ~2x performance improvement over the optimal single-threaded algorithm.

 

When factoring in the memory consumption, the optimal approach was to use FFTs for small multiplications that can fit into memory and only use NTTs/SSA for larger multiplications that do not. But in all cases, parallelization rarely netted more than ~2x speed improvement even on machines that had a lot more cores than that - which was very unsatisfying.

 

In other words: There was a need for a middle ground in the FFT vs. NTT space-time tradeoff to achieve any real performance gains.

 

 

Attempts to Find the Middle Ground:

 

Most attempts to achieve that middle ground involved iterating Karatsuba or Toom-Cook at the top level and using FFT. While this solves the problem of the FFTs using too much memory, it exacerbates the problem of memory bandwidth. So while this method lets you use FFT for larger products within a fixed memory budget, it does not actually improve performance and instead makes it worse.

 

 

The Algorithm

 

The solution turned out to be conceptually simple yet unobvious: Combine FFT with SSA to make the "Hybrid NTT".

 

Simple right? Yet in the 15 years that the existence of the Hybrid NTT was revealed to when this article was published, there appears to be no public evidence that Hybrid NTT was either reverse-engineered or independently rediscovered beyond some ideas in forum posts. (no implementations or critical details needed to make it efficient)

 

Since the Hybrid NTT combines the FFT and SSA, the rest of this article will assume you have an in-depth understanding of both algorithms. So links to their description will be provided (again) here:

(If you are new to bignum arithmetic, don't expect to quickly grasp either algorithm as they are very deep and involved. So I expect most readers to stop here.)

 

 

Structure:

 

Structurally, the Hybrid NTT uses the same SSA-style Fermat Transforms with numbers modulo 2N + 1. Thus the top-level of the algorithm is identical to SSA. The difference is how the pointwise products are done. While SSA normally recurses into either itself, Karatsuba/Toom-Cook, or Basecase multiplication, here we recurse into a negacyclic weighted floating-point FFT.

 

The use of negacyclic weighted FFT has a two-fold advantage:

The overall performance gain is tremendous as will be shown in the next section.

 

 

Performance

 

Due to the age of the Hybrid NTT and the retirement of the original computer used to develop it, no benchmarks could be run for the purpose of this article. So what you see here is taken from or derived from my records of many years ago. It makes no sense to use benchmarks on modern systems since computers have changed so much that they no longer show the significance of the Hybrid NTT.

 

Extending the table from earlier to include the Hybrid NTT we get the following on the same 2008-era 2 x Xeon X5482 server:

Algorithm Relative Computational Cost Relative Memory Requrements Relative Compute/Memory Ratio
Floating-Point FFT x86 + x64 1.0 4.0 0.25
32-bit Small Primes NTT x86 + x64 10.0 1.2 8.33
Schönhage-Strassen Algorithm (SSA) x86 10.0 1.0 10.00
x64 8.0 8.00
Hybrid NTT x86 3.0 1.0 3.00
x64 2.0 2.00

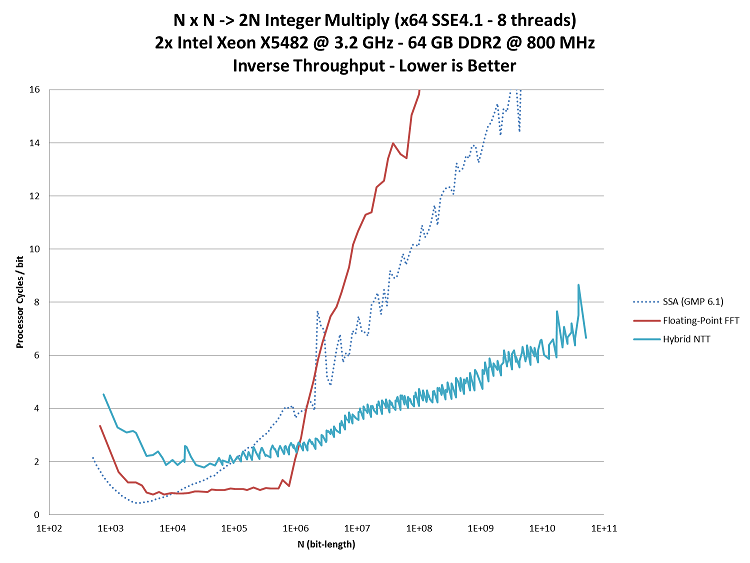
So while the Hybrid NTT was intended to be a middle-ground in a wide space-time tradeoff, it ended up becoming an uncompromising improvement. While it was still 2x slower than the FFT, it retains the high memory efficiency and is not memory-bound. Thus it scaled with parallelization. 2 threads was enough to overtake the FFT. 8 threads blew everything else out of the water.

 

The figure to the right captures the relative throughput of performing many independent multiplications of a specific size on all cores simultaneously. This type of benchmark closely represents the binary splitting workloads that appear when computing Pi and other constants.

 

To better visualize the data across such a large range of input sizes, the Y-axis has been scaled by the input size, but it is still linear.

 

GMP is provided as the state-of-the-art baseline.

 

At the small sizes, FFT is by far the fastest. But once it spills out of the CPU cache, its performance drops drastically as it falls behind even GMP's implementation of SSA.

 

In contrast, the Hybrid NTT's slowdown for spilling cache is very minimal and it performs well on ram.

 

 

Legacy:

 

The Hybrid NTT became the fastest known large multiplication algorithm for multi-core processors at the time. And for this reason alone, y-cruncher was created to see how many records could be smashed with it.

 

The first memory-efficient algorithm to beat the Hybrid NTT is the SSE4.1-optimized 32-bit Small Primes NTT.

 

While the Small Primes NTT is by no means a new algorithm, apparently nobody put together an optimized implementation using SSE4.1 instructions to test its speed. My own tests showed that it marginally outperformed the Hybrid NTT on 2008-2012 era hardware. And thus I put it into y-cruncher and activated it for the relevant processors.

 

The death blow for the Hybrid NTT came in 2013 with the release of the Haswell processor. Haswell* featured FMA3 and AVX2 instructions. AVX2 doubled the speed of the (already faster) 32-bit Small Primes NTT. Then FMA (Fused Multiply-Add) hardware enabled a new class of extremely fast algorithms of which y-cruncher's 2012-era VST algorithm was already related to and would eventually adapt.

 

The Hybrid NTT remained in y-cruncher until the v0.8.1 modernization effort where both the Hybrid NTT and the 32-bit Small Primes NTT were removed - thus taking with them the performance they provided for pre-FMA processors.

 

(*It's worth mentioning that AMD actually beat Intel to FMA hardware with Bulldozer in 2011. However, this was a difficult time for AMD as their Bulldozer processor line had poor performance compared to what Intel had to offer at the time. Thus AMD processors didn't get as much developer attention.)

 

 

The Devil is in the Details

 

While the Hybrid NTT can be described in one sentence, actually implementing it presents a different set of challenges. Maybe this is why nobody else has tried it? But let's start by defining the transform parameters of the Hybrid NTT.

 

 

Fermat Transform Parameters:

 

The Fermat Transform component of the Hybrid NTT has 2 core parameters and 3 derived parameters (as implemented in y-cruncher):

 

Core Parameters:

k describes the length of the transform as a power-of-two. Thus the transform length is 2k points.

m is a "multiplier" that describes the point-size as a multiple of the minimum size for that transform length.

 

Derived Parameters:

Nb and N give the size of the points in bits and 32-bit words respectively. The Fermat Transform thus operates in the modulo (2Nb + 1). y-cruncher's implementation uses 32-bit words. This is the case even on x64 as the algorithm was written in the 32-bit days and never properly re-optimized for 64-bit.

 

wb gives the number of operand words to place into each point. After convolution, the coefficients can be as large as (32*2*wp + k) bits long. (wp = Nb / 64 - 1) is chosen because it is the largest value such that (32*2*wp + k < Nb).

 

Here is a sample of some possible transform parameters:

Basic Parameters Derived Parameters Maximum Product Size

k

m

Nb (point size in bits)

N (point size)

wp (words/point)

 Bits

Decmial digits

9

1

128

4

1

16,384

4,932

9

2

256

8

3

49,152

14,796

9

3

384

12

5

81,920

24,660

9

4

512

16

7

114,688

34,524

9

5

640

20

9

147,456

44,388

10

1

256

8

3

98,304

29,592

10

2

512

16

7

229,376

69,049

10

3

768

24

11

360,448

108,505

10

4

1,024

32

15

491,520

147,962

10

5

1,280

40

19

622,592

187,418

11

1

512

16

7

458,752

138,098

11

2

1,024

32

15

983,040

295,924

11

3

1,536

48

23

1,507,328

453,750

11

4

2,048

64

31

2,031,616

611,577

11

5

2,560

80

39

2,555,904

769,403

12

1

1,024

32

15

1,966,080

591,849

12

2

2,048

64

31

4,063,232

1,223,154

12

3

3,072

96

47

6,160,384

1,854,460

12

4

4,096

128

63

8,257,536

2,485,766

12

5

5,120

160

79

10,354,688

3,117,071

The purpose of the m parameter is to give more granularity to the available transform sizes. Without it, the only available transform sizes are powers-of-4 apart.

In all cases, N must be a multiple of 4 to retain word-alignment and to prevent the butterfly routines from degenerating.

Transform lengths as short as 24 are allowed in y-cruncher provided that the multiplier is set such that N is an integer for word alignment.

 

 

Pointwise Multiplication via Negacyclic FFT Convolution:

 

As mentioned earlier, classic SSA performs these pointwise products using either Basecase multiplications, Karatsuba/Toom-Cook, or recursively into itself. But of course we're gonna do it much better using floating-point FFT.

 

The main difficulty here is getting the FFT convolution length to exactly match the number length of the Fermat Transform points. While this is not required to use FFT for the pointwise products, it is needed to achieve the 2x speedup of negacyclic wrap-around via weighted convolution.

 

In other words:

Nb = convolution_lengthFFT

Setting the convolution length of the FFT to match that of the Fermat Transform point-size is not a trivial task. And it is probably one of the more difficult and tricky problems that stand in the way of the Hybrid NTT algorithm.

 

 

There are two known viable approaches to do this:

The IBDWT method is more flexible in that it allows the FFT to match any convolution length. However, the method was not known to me when the Hybrid NTT was implemented back in 2008. So we will proceed with the "meet-in-the-middle" length matching method.

 

 

For a given FFT of transform length lengthFFT that puts wFFT bits per FFT word:

Nb = wFFT * lengthFFT

Of course, we can't just use any length FFT. Not all FFT lengths are efficient. y-cruncher only supports FFT lengths of the form (m * 2k) where m is 1, 3, or 5.

Nb = wFFT * mFFT * 2kFFT

When we substitute in the Fermat Transform parameters for Nb, we finally get something useful:

mFNT * 2k-2FNT = wFFT * mFFT * 2kFFT

 

So in order to use negacyclic convolution, the parameters of the Fermat Transform and the FFT must satisfy the following equation and constraints:

mFNT * 2k-2FNT = wFFT * mFFT * 2kFFT

 

mFFT = 1, 3, or 5

 

wFFT must be small enough to avoid round-off errors in the FFT. Typical values are 12 - 18.

 

So we are trying to solve a cost minimization problem while satisfying a 5-variable discrete equation with additional constraints. That's actually quite difficult to solve - especially due to the lack of a cost model. So we don't even try. The solutions are pre-computed and dumped into a massive lookup table that is compiled into the code.

 

Some reasonable questions to ask at this point are:

  1. Are these constraints too tight?
  2. Are there enough solutions to provide a sufficient number of usable transforms?
  3. Are the solutions even efficient in practice?

In short the answers are no, yes, and sometimes. There are enough efficient solutions to make negacyclic convolution viable for most number ranges.

 

The constraints are not too tight. 2k-2FNT and 2kFFT provide full flexibilty for scaling by multiples of two. mFNT is the key to achieving granularity between powers of two. And the non-factors of two in mFNT can be split into wFFT and mFFT.

 

For example, kFNT = 14 has 10 million digit granularity. And all but 4 multipliers up to 32 can be achieved.

Step

Product Size (Decimal)

Fermat Number Transform Mode

Pointwise FFT Mode

kFNT

mFNT

Nb

kFFT

mFFT

wFFT

4

40,087,909

15

1

8,192

9

1

16

5

50,346,626

14

5

20,480

8

5

16

6

60,447,516

14

6

24,576

9

3

16

7

70,548,407

14

7

28,672

11

1

14

8

80,491,471

15

2

16,384

10

1

16

9

90,750,188

14

9

36,864

11

1

18

10

100,851,078

14

10

40,960

9

5

16

11

110,951,969

14

11

45,056

12

1

11

12

120,895,033

15

3

24,576

9

3

16

13

131,153,750

14

13

53,248

12

1

13

14

141,254,640

14

14

57,344

12

1

14

15

151,355,531

14

15

61,440

12

1

15

16

160,982,942

16

1

16,384

10

1

16

17

171,557,312

14

17

69,632

12

1

17

18

181,658,202

14

18

73,728

12

1

18

19

Not Possible

20

201,702,157

15

5

40,960

9

5

16

21

211,960,874

14

21

86,016

11

3

14

22

222,061,765

14

22

90,112

13

1

11

23

Not Possible

24

242,105,719

15

6

49,152

10

3

16

25

252,364,436

14

25

102,400

11

5

10

26

262,465,327

14

26

106,496

13

1

13

27

272,566,217

14

27

110,592

11

3

18

28

282,509,281

15

7

57,344

12

1

14

29

Not Possible

30

302,868,889

14

30

122,880

13

1

15

31

Not Possible

32

322,597,190

16

2

32,768

11

1

16

Not surprisingly, the ones that are not possible are when mFNT is a large prime number since it cannot be divided across wFFT and mFFT.

However, not all of the achievable modes that are available in this table are actually efficient. For example, step 27 is likely to be faster than step 25 because it has a much higher FFT efficiency at 18 bits-per-point vs. 10 for step 25.

 

These "reversals" can be highly dependent on the processor environment - which makes the minimization problem more difficult to solve. The lack of a cost model makes it difficult to determine what modes are faster than others. And to make matters worse, it varies by processor. So in the end, y-cruncher doesn't even try to solve it directly. It uses a super-optimizer.

 

 

Super-Optimizer:

 

The super-optimizer is actually a lot more boring than the name suggests. It doesn't do anything "super". Instead, it's just brute-force. That is, benchmark all possible transform modes, pick the most efficient ones, then throw them into a lookup table.

 

Needless to say, these tables can vary drastically across processors and thus each will have their own customized table.

 

The brute-force nature of the super-optimizer means there could be an exponentially large search space to test depending on how many parameters it is allowed to probe. Therefore some amount of manual guiding is needed to skip entire classes of obviously bad inputs and restrict the search to only areas that are likely to produce efficient results. Nevertheless, the super-optimizer still takes many hours to even days to run depending on the speed of the processor(s) and how large you want to optimize to. Best results are usually obtained with the highest possible end processor with a maxed out memory configuration.

 

In the absence of the super-optimizer table (such as for sizes that are too large to be tested), a heuristic is used to choose parameters. But the lack of a good cost model means that these heuristically chosen parameters often underperform super-optimizer parameters by 30% or more.

 

The hybrid nature of the Hybrid NTT and how it combines integer and floating-point computation makes it difficult to build such cost model. Processors vary drastically in their relative integer vs. floating-point performance. And to make things worse, cache sizes also play a large part. Analysis of super-optimizer results show that the optimal values for Nb are strongly correlated with the various levels of cache. The point here is to forget about the cost model and rely on benchmarks instead.

 

Going beyond the Hybrid NTT, super-optimization is also used in y-cruncher's other large algorithms - though with lesser effect until recent years. None of these other algorithms are quite as heterogeneous as the Hybrid NTT and thus are easier to build cost models for.

 

 

Limitations

 

As mentioned at the start of this article, the Hybrid NTT has been obsolete since 2013. Or specifically, it has been obsolete on processors made after 2013. There are two main limitations that prevent the Hybrid NTT from running well on newer hardware.

 

 

Fermat Transforms are not Vectorizable until AVX512:

 

Modern computer hardware features wide SIMD instructions like AVX and AVX512. Thus in order to fully utilize modern processors, code must be able to use SIMD instructions.

 

While the pointwise products are easily vectorizable with SIMD since they are floating-point FFTs, the same cannot be said about the Fermat Transforms. The problem is of course the carry propagation within the arithmetic modulo (2Nb + 1). Carry propagation has cross-lane dependencies which prevent vectorization. While these dependencies can be broken by means of redundant representations, it is difficult to do it without either drastically increasing memory usage or breaking up data alignment and screwing up other parts of the algorithm.

 

Things change with AVX512 thanks to the Kogge-Stone Vector Adder which allows carry-propagation to be vectorized. But with competition from more modern algorithms, it's too little, too late.

 

 

Fermat Transforms are not Cache Efficient at Large Sizes:

 

While the inability to vectorize is bad, it is not actually fatal to the algorithm. This one is however.

 

Fermat Transforms do arithmetic modulo (2Nb + 1) which is a "large" number. At best, these are no smaller than the square root of the convolution length. This means that at sufficiently large sizes, a single point will be larger than the CPU's cache. And once that happens, performance falls off a cliff - so much so that it even becomes CPU-bound in disk-swapping computations. (meaning that it's slower than disk)

 

For CPU hardware of eras 2008-2023, this begins to happen at around 500 billion digits. While this is much larger than what most applications will reach, y-cruncher of course is not your typical application and is expected to multiply numbers much larger than that.

 

Fundumentally, this problem makes it impossible to build a cache oblivious implementation thus making it asympotically worse than other FFT-based algorithms in terms of run-time complexity.

 

 

 

 

Possible Improvements

 

There are some potential extensions and improvements to the Hybrid NTT which were never implemented in y-cruncher. As the algorithm has become obsolete, there is no intention to implement anything here and will remain only for academic purposes.

 

 

Irrational Base Discrete Weighted Transform:

 

This was mentioned earlier in this article. The idea is to use the Irrational Base Discrete Weighted Transform (IBDWT) to perform the pointwise multiplications.

 

The irrational base nature of them allows the FFT to achieve any convolution length. Thus there is no longer a need to play the meet-in-the-middle game with the Fermat Transform parameters. Furthermore, it allows all the remaining transform lengths which were formerly not possible. The result is of course, finer-grained and more efficient transforms for arbitrary input sizes.

 

The drawback here is the need for weights. And unlike twiddle factors, these weights will vary for each set of parameters. No research has been done in this area to see what the consequences of this are and whether it needs to be dealt with in some way.

 

 

Truncated FFT Algorithm:

 

The meet-in-the-middle length matching and IBDWT approaches are just different ways to solve the same problem - that is, to multiply large numbers that don't efficiently fit into an available set of transform parameters. (In other words, smooth out the performance curve so the step-function effect is less bad.)

 

An alternate approach to achieving arbitrary product sizes is to use the Truncated FFT algorithm (TFT).

 

Libraries like FLINT have shown that the TFT is able to achieve very smooth performance curves off a very rigid set of base transforms. (much better than what is achieved by the Hybrid NTT implementation described in this article)

 

Overall, the TFT is not something that I have personally researched in depth due to two drawbacks:

For now (even for modern post-Hybrid NTT algorithms), there are simpler approaches for smoothing out the performance curve that are almost as good.

 

 

Kogge-Stone Vector Adder:

 

Mentioned in an earlier section, the Fermat Transform arithmetic modulo (2Nb + 1) requires carry propagation which is normally not vectorizable. AVX512 finally makes it possible to vectorize it.

 

 

3-way Hybrid NTT:

 

For super large multiplications (above ~100 billion digits), the pointwise multiplications become so large that the FFTs begin to spill cache. So at this point, the Hybrid NTT loses efficiency very quickly as the sizes increase.

 

The solution to this is to have the Hybrid NTT recurse into itself like the SSA algorithm. However, this runs into a similar length matching problem where the recursive Fermat Transforms need to match the convolution length of the pointwise products of the main one. The problem is - this one is even tricker to solve.

 

Recall that the Fermat Transform is done modulo (2Nb + 1). Thus we need a convolution length of exactly Nb bits, which we already showed how to do using floating-point FFTs. The problem is that this is much harder to achieve using a 2nd layer of Fermat transforms.

 

The Fermat Transform parameters we have chosen so far are:

Which leads to a convolution length of (m * 22k - 3 - 32) bits. So the equality which must be achieved is:

M = m for top-level Fermat Transform

K = k for top-level Fermat Transform

 

m = m for lower-level Fermat Transform

k = k for lower-level Fermat Transform

 

M * 2K-2 = m * 22k - 3 - 32

You can probably already see the problem. That -32. ugh... Both (M * 2K-2) and (m * 22k - 3) are highly composite. That -32 ruins any possibility of easily satisfying this equality. Even worse, the IBDWT cannot save us here since we are now in an integer ring that lacks the necessary square-root-of-two weights. We're screwed right?

 

Not exactly... But before we get into the solution, it's worth asking where did the -32 come from? It comes from the -1 in (wp = Nb / 64 - 1). The -1 here is the extra 32 bits of space needed to hold the large coefficient of the output polynomial. (since all these FFT-based algorithms are just polynomial multiplication algorithms prior to carryout) Thus while we want to use the full with of Nb, we can't because we need to reserve space to hold the coefficients being slightly larger.

 

It turns out the trick here that saves us is to incorporate the 3rd FFT-based algorithm - the Small Primes NTT.

 

In order to use the full width of Nb without sacrificing any bits to hold the k extra bits of data, we expand it by CRT'ing (Chinese Remainder Theorem) it with an NTT modulo a small prime. For the purposes here, modulo the Fermat prime (216 + 1) will suffice for anything that fits on current computers.

 

Thus to perform a negacyclic convolution of exactly (M * 2K-2) bits, we need to:

  1. Select k and m to satisfy (M * 2K-2 = m * 22k - 3). This should be trivial.
  2. Break the (M * 2K-2) bits into a polynomial of degree (2k - 1) with (M * 2K-2)/2k bits per term. Call this I(x).
  3. Perform negacyclic Hybrid NTT of I(x) with parameters k and m. Skip the carryout at the end and leave as polynomial coefficients modulo (2Nb + 1). Call it H(x).
  4. Reduce all the coefficients of I(x) modulo (216 + 1). Call it S(x).
  5. Perform negacyclic regular NTT of S(x) with transform length 2k. Skip the carryout at the end and leave as polynomial coefficients modulo (216 + 1). Call it N(x).
  6. CRT combine the coefficients of H(x) and N(x) to get O(x). (2Nb + 1) should be relatively prime to (216 + 1) for all the possible inputs that we allow.
  7. Perform carryout on O(x) with radix (M * 2K-2)/2k.

And so, we have pulled off a trifecta - a hybrid algorithm that combines all 3 of the major FFT-based multiplication algorithms!

 

 

Here is an example parameter selection of a very large 2-stage Hybrid NTT using this 3-way hybrid algorithm. The important numbers that need to be matched are bolded.

 

 

Top-Level Fermat Transform:

The pointwise products will require negacyclic convolution of length 402,653,184 bits. This is too large to efficiently do using floating-point FFT. So we will do it using an element-wise CRT of two transforms.

 

 

Mid-Level Fermat Transform:

 

Mid-Level Small NTT:

 

Bottom-Level Floating-Point FFT: