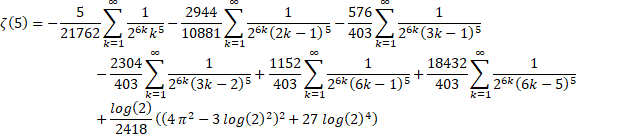News (2019)
Back To:
Second Formula for Zeta(5): (November 1, 2019) - permalink
Oliver Kruse has managed to unearth a new formula for Zeta(5) based on one of the original BBP papers. As far as I can tell, this formula is mathematically independent from Broadhurst's formula from 1998. Thus we finally have two different formulas for Zeta(5).
Moving forward, it is no longer permitted to use two versions of Broadhurst's formula as compute/verify pairs as had been done in the records to date.
Therefore, the fastest pair of allowed formulas for Zeta(5) records are:
The formula file for the new formula will be bundled into the next patch or release of y-cruncher.
With some basic optimizations, the new formula looks like this:
Version 0.7.8 Public Beta: (October 5, 2019) - permalink
Version 0.7.8 is now available as a public beta and release candidate. More information here.
This is unusual since I normally just push new versions out. But the changes in v0.7.8 are large and intruisive enough that I want some public user-testing before anybody tries to do anything crazy with it. (i.e. setting world records)
Technology Wishlist: (June 24, 2019) - permalink
For some number of years, I kept a mental list of hardware improvements that could benefit the project in some way. This list includes pretty much anything that's hardware-related since those are generally beyond my control. So stuff like faster hard drives, high endurance SSDs, and instruction set extensions...
The full page is here. And I will probably keep it updated as things change.
To be clear, these are feature requests. But I have no expectation that any of them will ever happen.
Commercial Use Reminders: (April 22, 2019) - permalink
Due to the amount of publicity that Google's latest computation has generated, there are multiple parties who have expressed interest in doing the same thing - that is to advertise a product or service by setting a world record for Pi.
As unpopular as this will sound, I must remind everyone (including those who have not reached out to me) that y-cruncher is not free for such commercial use. So if you wish to repeat what Google did, you too will need to acquire a commercial use license.
To put it frankly, corporations are not allowed to profit off my work for free unless it falls under one of the exceptions. In the past, I've typically allowed minor violations to slip since I usually don't care and I'm not exactly the kind of person to chase people down. But things are starting to get out of hand now.
Google Cloud Topples the Pi Record: (March 14, 2019) - permalink
Happy Pi Day everyone!
Guess what? Records are meant to be broken and there is a new one!
From September to January, Emma Haruka Iwao of Google (@Yuryu) ran a computation of Pi to 31.4 trillion digits. The exact number of digits that was computed is 31,415,926,535,897 decimal digits and 26,090,362,246,629 hexadecimal digits. (Pop Quiz: Where do those figures come from?)
The details of the computation can be found in the main article. Below are the official Google blogs:
Version v0.7.7: (January 5, 2019) - permalink
Version 0.7.7 is now out and with it are all mathematical features that I've blogged about here months ago.
- The Custom Formula feature along with about 80 prebuilt formulas and constants.
- 3 new built-in algorithms for Catalan's constant: Guillera, Pilehrood-short, and Pilehrood-long
- A new built-in algorithm for the Lemniscate constant: AGM-Pi
So for the first time in years, this is a major release with almost nothing on the hardware/optimization front.
The defining feature for this release is obviously the custom formulas. As mentioned in the October blog, it allows y-cruncher to evaluate user-input formulas.
The final list of functions for v0.7.7 is:
- Basic Arithmetic: addition, subtraction, multiplication, division, integer power
- Elementary Functions: square root, arithmetic-geometric mean (AGM), logarithms, ArcCoth() of integer
- Special Functions: ArcSinlemn() of rational, generalized hypergeometric series of rationals
- Constants: Golden Ratio, e, Pi, Zeta(3), Catalan's Constant, Lemniscate, Euler-Mascheroni Constant
The only thing new since the original announcement is that the logarithm has been extended to allow any real input as opposed to just small integers.
All of these operations are fully parallelized and run in quasi-linear time and linear memory. There is also support for swap mode and checkpoint restart. Thus anything that can be represented (or sufficiently approximated) by a reasonably small combination of these operations (subject to restrictions) can be now be feasibly computed to billions or even trillions of digits without being limited by physical memory. This is well beyond the capability of most computer algebra systems. So hopefully it will serve as a useful tool for researchers in search of algorithms for super-high-precision computation of various constants and functions.
The download bundles now include about 80 prebuilt formulas which you can input into y-cruncher to compute. Feel free to contribute more on GitHub.
Documentation for the custom formulas can be found here.
Due to the sheer size and scope of the custom formulas, I expect there to be a lot of bugs. So if you encounter anything that doesn't seem right, let me know either though email or by opening an issue on GitHub.