News (2024)

 

Back To:

 

Countering the Compiler Regression with Optimizations: (April 3, 2024) - permalink

 

These kind of topics are hard to write about since it's not all positive. But let's start with a table because everyone hates walls of text:

Processor Architecture Clock Speeds Binary ISA 1 Billion Digits of Pi (times in seconds)
v0.8.4 v0.8.5 (ICC) v0.8.5 (ICX) v0.8.4 -> v0.8.5 ICC -> ICX Overall
Core i7 920 Intel Nehalem 3.5 GHz + 3 x 1333 MT/s 08-NHM x64 SSE4.1 535.818 492.971 482.982 +8.00% +2.03% +9.86%
Core i7 3630QM Intel Ivy Bridge stock + 2 x 1600 MT/s 11-SNB x64 AVX 339.96 318.037 305.360 +6.45% +3.99% +10.18%
FX-8350 AMD Piledriver stock + 2 x 1600 MT/s 12-BD2 x64 FMA3 225.749 218.338 216.159 +3.28% +1.00% +4.25%
Core i7 5960X Intel Haswell 4.0 GHz + 4 x 2400 MT/s 13-HSW x64 AVX2 49.441 48.568 50.205 +1.77% -3.37% -1.55%
Core i7 6820HK Intel Skylake stock + 2 x 2133 MT/s 14-BDW x64 AVX2 + ADX 102.144 100.887 103.570 +1.23% -2.66% -1.40%
Ryzen 7 1800X AMD Zen 1 stock + 2 x 2866 MT/s 17-ZN1 x64 AVX2 + ADX 77.505 75.965 76.800 +1.99% -1.10% +0.91%
Core i9 7940X Intel Skylake X 3.6 GHz (AVX512) + 4 x 3466 MT/s 17-SKX x64 AVX512-DQ 20.686 19.912 20.428 +3.74% -2.59% +1.25%
Ryzen 9 3950X AMD Zen 2 stock + 2 x 2666 MT/s 19-ZN2 x64 AVX2 + ADX 34.814 33.292 33.161 +4.37% +0.39% +4.75%
Core i7 11800H Intel Tiger Lake stock + 2 x 3200 MT/s 18-CNL x64 AVX512-VBMI 35.739 34.438 35.052 +3.64% -1.78% +1.92%
Ryzen 9 7950X AMD Zen 4 stock + 2 x 5000 MT/s 22-ZN4 x64 AVX512-GFNI 18.978 18.848 18.937 +0.69% -0.47% +0.22%

ICC is Intel's old Classic C++ Compiler (ICC). And ICX is Intel's new LLVM Compiler (ICX). So we can see that:

  1. y-cruncher v0.8.5 will have new software optimizations that improves performance on all processors.
  2. Intel's new compiler (ICX) is worse than their old compiler (ICC) on nearly all modern processors.

In short, Intel's new compiler is causing a performance regression in y-cruncher. In order to prevent the next version of y-cruncher from actually getting slower, I am trying to offset the regressions with new performance optimizations - with only partial success so far.

 

 

But how did we get here?

 

Intel's classic C++ compiler has historically been the best compiler for code performance. However, starting from about 2020, Intel began migrating to a new LLVM-based compiler (ICX) which they wrapped up last year by discontinuing their old compiler (ICC). The problem is that for y-cruncher at least, ICX isn't actually better than ICC.

Processor Architecture Clock Speeds Binary ISA BBP - 10 billionth Hex Digit of Pi (times in seconds)
MSVC 17.7.1 ICC 19.2 ICX 2024 ICC -> ICX
Core i7 920 Intel Nehalem 3.5 GHz 08-NHM x64 SSE4.1 568.384 574.745 725.910 -26.30%
Core i7 3630QM Intel Ivy Bridge stock 11-SNB x64 AVX 525.811 436.337 464.628 -6.48%
FX-8350 AMD Piledriver stock 12-BD2 x64 FMA3 251.695 231.205 235.828 -2.00%
Core i7 5960X Intel Haswell 4.0 GHz 13-HSW x64 AVX2 55.249 50.640 53.422 -5.49%
Core i7 6820HK Intel Skylake stock 14-BDW x64 AVX2 107.977 105.307 108.959 -3.47%
Ryzen 7 1800X AMD Zen 1 stock 17-ZN1 x64 AVX2 97.809 97.915 95.269 +2.70%
Core i9 7940X Intel Skylake X 3.6 GHz (AVX512) 17-SKX x64 AVX512-DQ 13.518 13.561 15.340 -13.12%
Ryzen 9 3950X AMD Zen 2 stock 19-ZN2 x64 AVX2 22.506 21.043 20.982 +0.29%
Core i7 11800H Intel Tiger Lake stock 18-CNL x64 AVX512-DQ 50.002 50.798 51.654 -1.69%
Ryzen 9 7950X AMD Zen 4 stock 22-ZN4 x64 AVX512-DQ 11.521 11.424 12.232 -7.07%

In other words, Intel got rid of their old compiler while their new compiler has yet to match it in performance. And because of the need to stay up-to-date with C++ features and CPU instruction sets, I cannot stay on an old compiler forever. Thus an "upgrade" is inevitable even if that hurts performance.

 

What about other compilers? If Intel's new compiler is bad, what about other alternatives? Well...

So even though Intel has made their compiler worse, it's still better than its competitors.

 

 

So why is Intel's new compiler worse than their old compiler?

 

There is no single regression in Intel's LLVM compiler that is responsible for the entire regression vs. their classic compiler. It's a combination of many regressions (and improvements) that collectively add up with the regressions winning in the end by several %. Anecdotally speaking, small regressions tended to involve inferior instruction selection and ordering while larger regressions tended to fall into these categories:

This last category is particularly nasty. Complicated loop optimizations like loop-interchange, loop fusion/fission, loop materialization, aggressive loop unrolling, etc... are only turned on at maximum optimization level (O3) for most compilers due to their high risk of backfiring. However, I've observed that most of these are already enabled at O1 and O2 for ICX and are difficult or impossible to disable. And when such optimizations backfire, it can kill performance of the loop easily by a factor of 3x or more.

 

Below are some pseudo-code examples illustrating major ways that I have observed ICX loop optimizations to backfire. Actual code that experiences such behavior are generally much larger and more complicated in size. Self-contained samples have been provided to Intel's engineers in the hope that they can improve their compiler.

 

 

Example 1: Loop Fusion Gone Bad

 

    double* A = ...;

    for (size_t c = 0; c < length; c++){

        double tmp = A[c];

 

        //  Long dependency chain.

 

        A[c] = tmp;

    }

    for (size_t c = 0; c < length; c++){

        double tmp = A[c];

 

        //  Long dependency chain.

 

        A[c] = tmp;

    }

In this example, the iterations of each loop are all independent and can be run in parallel. But within each iteration is a long dependency chain. In order to keep the iterations within the CPU reorder window, the work is intentionally split into multiple loops (more than just 2 loops as shown here). This allows the CPU to reorder across iterations - thus allowing instruction level parallelism.

 

However, ICX doesn't always allow this to happen. Instead, it sometimes decides to undo my hand optimization by fusing the loops back together into this:

 

    for (size_t c = 0; c < length; c++){

        double tmp = A[c];

 

        //  Super long dependency chain.

 

        A[c] = tmp;

    }

While this improves memory locality by traversing the array only once instead of twice. It has increased the dependency chain to the point that the CPU is no longer able to sufficiently reorder across iterations. Thus it kills instruction-level parallelism (ILP) and hurts performance. The compiler may be incorrectly assuming that the dataset does not fit in cache when in fact it does.

 

The same situation can happen with loop-interchange where ICX will interchange loops to improve memory locality at the cost of creating dependency chains that wipe out instruction level parallelism.

 

 

Example 2: Everything Blows Up

 

This example is a pathologically bad case where Loop-invariant Code Motion (LICM) and loop unrolling combine to create a perfect storm that simultaneously blows up instruction cache, data cache, and performance. While it looks rather specific, it is nevertheless a common pattern in y-cruncher.

 

Here the code is iterating an array of AVX512 vectors that uses 1000 scalar weights. Each time a scalar weight is used, it is broadcast to a full vector to operate on the array A. In AVX512, a scalar broadcast has the same cost as a full vector load. So there is no added cost of redoing the broadcast in the inner loop.

 

    const double* weights = ...;

    __m512d* A = ...;

    for (size_t c = 0; c < length; c++){

        __m512d tmp = A[c];

 

        for (size_t w = 0; w < 1000; w++){

            __m512d weight = _mm512_set1_pd(weights[w]); //  Scalar Broadcast. Same cost as regular load.

            //  Do something with "tmp" and "weight".

        }

 

        A[c] = tmp;

    }

 

Instead, ICX has a tendency to turn it into the following:

 

    const double* weights = ...;

    __m512d* A = ...;

 

    __m512d expanded_weights0 = _mm512_set1_pd(weights[0]); //  Each of these is 64 bytes!

    __m512d expanded_weights1 = _mm512_set1_pd(weights[1]);

    __m512d expanded_weights2 = _mm512_set1_pd(weights[2]);

    ...

    __m512d expanded_weights999 = _mm512_set1_pd(weights[999]);

 

    for (size_t c = 0; c < length; c++){

        __m512d tmp = A[c];

 

        //  Do something with "tmp" and "expanded_weights0".

        //  Do something with "tmp" and "expanded_weights1".

        //  Do something with "tmp" and "expanded_weights2".

        //  ...

        //  Do something with "tmp" and "expanded_weights999".

 

        A[c] = tmp;

    }

What was supposed to be a bunch of (free) scalar broadcasts has turned into 64 KB of stack usage and two fully unrolled 1000-iteration loops - one of which is completely useless. In this example, this transformation is never beneficial as broadcast loads are already free to begin with. So replacing them with stack spills and trashing both the data and instruction caches only makes things worse. For small values of length, this transformation is devastating to performance due to the initial setup.

 

So what happened?

  1. The compiler first sees that the inner loop has a compile-time trip count. So it decides it can completely unroll it. I have never seen compilers completely unroll loops this large, but ICX apparently does it with several of y-cruncher's kernels.
  2. The compiler deduces that weights does not alias with A. Thus it sees that the loads and scalar broadcasts are loop invariant. So it pulls them out of the loop. Yes, all 1000 of them.
  3. Those 1000 values need to go somewhere right? So it spills them onto the stack (and also incurring any penalties due to stack misalignment).

To put it simply, other compilers do not do this kind of stuff. Or at least they have limits to prevent this from happening. ICX appears to be completely unrestrained.

 

A common theme among ICX misoptimizations is that Loop Invariant Code Motion (LICM) and Common Subexpression Elimination (CSE) will create additional live values that end up getting spilled to the stack, thus invoking a penalty that is often larger than the initial savings. The example above is a cherry-picked example where ICX takes this concept to the extreme resulting in an avalanche of secondary regressions such as misalignment penalties and cache pollution.

 

 

Conclusion:

 

Intel's LLVM compiler is undoubtly a very powerful compiler. And the more I study it, the more I am impressed with its ability. However, with power comes responsibility, and unfortunately I cannot say that ICX wields this power well. I have yet to investigate if these issues are in LLVM itself or in Intel's modifications to it. But regardless, as of today, Intel's LLVM compiler can be best described as a child running with scissors - young and reckless with dangerous tools.

 

How long will it take for ICX to reach ICC's qualty of code generation? I have no idea. And after waiting more than a year for this to happen, I've decided that it's probably not going to happen for a very long time. For every thing that ICX screws up, it probably gets 5 others right. But for code that has already been hand-optimized, getting it right is neutral while getting it wrong hurts a lot. Dropping down to assembly is not an option because there are "thousands" of distinct kernels which are largely generated via template metaprogramming.

 

Is y-cruncher the only application affected like this? Probably not.

 

 

 

 

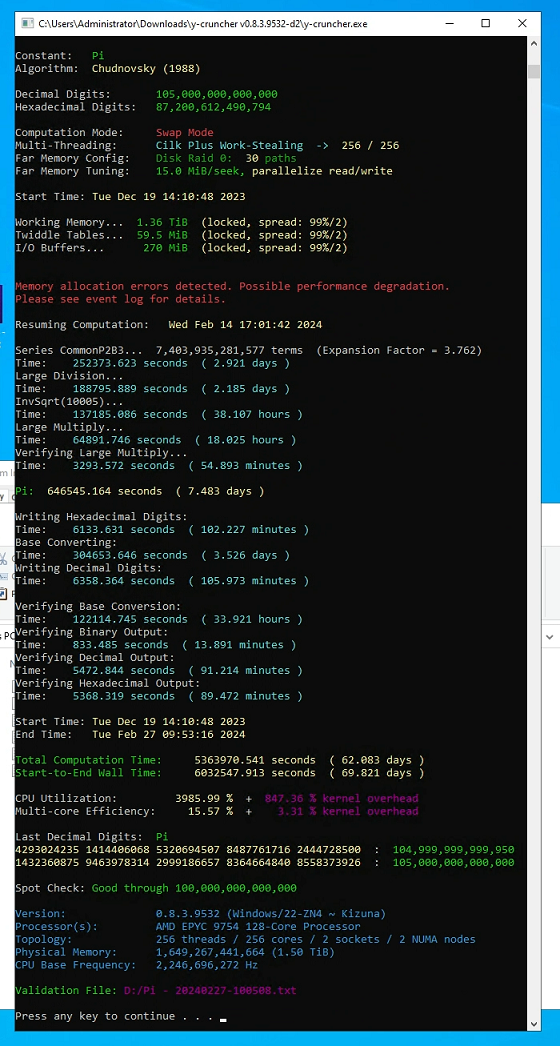
Limping to a new Pi Record of 105 Trillion Digits: (March 14, 2024) - permalink

 

If the bug that was fixed in v0.8.3.9533 made you suspect something was happening, you were right.

 

Jordan Ranous from StorageReview has followed up last year's speedrun of Pi with a record this time: 105 trillion digits of Pi

 

Originally, this was supposed to be another speedrun with slightly more digits to set the record. But it turned into anything but that as it ran into a multitude of problems. So unlike the majority of the past Pi records done with y-cruncher, this one did not go smoothly. And for the first time in over 10 years, a Pi record attempt required developer intervention to complete. So unlike the majority of past records, I was very much involved in this one.

 

But in the end, a record is still a record. It doesn't need to be pretty.

 

 

Computation:

Decimal Digits: 105,000,000,000,000
Total Time:

75 days

(December 14, 2023 - February 27, 2024)
CPU: 2 x AMD Epyc 9754 Bergamo (256 cores, SMT off)
Memory: 1.5 TB DDR5
Storage:

Swap: 30 x Solidigm P5316

Digit Output: 6 x Solidigm P5316
OS: Windows Server 2022 (21H2)
Software: y-cruncher v0.8.3.9532 (with developer fixes)
Validation File: Validation File

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Verification (x2):

Total Time:

4 days

(January 2, 2024 - January 6, 2024)
CPU: Intel Core i9 7900x @ 3.6 GHz (AVX512)
Memory: 128 GB DDR4
OS: Windows 10 (22H2)
Software: y-cruncher v0.8.4 (early development build)
Screenshot: Screenshot

 

 

 

 

 

 

 

 

 

 

 

 

The Original Plan:

 

As stated, the goal was to repeat last year's 100 trillion digit speedrun, but with better hardware and better software:

  Last Year's 100 Triillion Digit Speedrun This 105 Trillion Digit Record Run
CPU:

2 x AMD Epyc 9654 (Genoa)

192 Cores

2 x AMD Epyc 9754 (Bergamo)

256 Cores
Memory: 1.5 TB DDR5 1.5 TB DDR5
Storage: 19 x Solidigm P5316 36 x Solidigm P5316
Software: y-cruncher v0.7.10.9513 y-cruncher v0.8.3.9532 + fixes

 

 

 

 

 

 

 

 

 

 

 

 

 

The main improvements were the larger number of cores, greater storage bandwidth, and all the recent improvements to y-cruncher including the SSD ones.

 

This was supposed to only take a month, but as mentioned, things did not go as planned and it ended up dragging out for more than 2 months - longer than last year's computation.

 

 

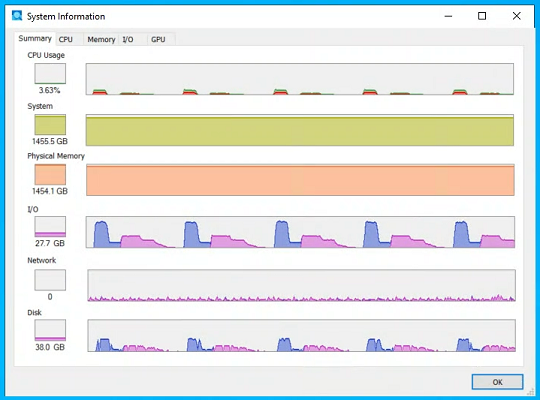
Below Expected Performance:

 

A couple weeks into the computation, the first thing that began to go awry was the performance.

Poor Sustained I/O Bandwidth

(blue = read, purple = write)

 

 

Non-direct Attached Storage:

 

The first problem was the indirect attached storage. In last year's computation, all 19 SSDs were direct attached to the motherboard. In this computation, 30 SSDs were used for swap of which 6 were direct attached while the remaining 24 were external and connected via a pair of PCIe connections. It is these PCIe connections that became the bottleneck.

 

The result is that 6 of the SSDs were very fast while the remaining 24 were slow. Thus on every burst of I/O, the bandwidth would start fast. Once the 6 fast SSDs finished, the remaining 24 were still running at a much lower speed.

 

Write bandwidth was also poor due to QLC SSDs having inconsistent performance depending on the state of their SLC cache. So on every burst of writes, there would always be 1 or 2 SSDs which take much longer to finish than the rest (i.e. "stragglers"). And the nature of RAID-0 is that performance is bottlenecked by the slowest drive.

 

It's unclear if this is a regression from last year's run, but it certainly didn't show up during the pre-run I/O benchmarks when the SSDs were mostly empty and had a clean cache state.

 

 

Amdahl's Law and Zen4 Hazard:

 

The second problem was the Amdahl's Law and Zen4 Hazard problem. While we knew this would be a problem before starting the run, the fix for it was not going to be ready for months. But since this problem has already existed for years, it isn't considered a regression from last year's 100 trillion digit speedun. But it did contribute to missing the original 1 month target.

 

As of today, we're unable to quantify how much it slowed down the computation. But empirically speaking, whenever Jordan checked on the computation, it was showing 0% CPU+disk utilization more often than not. And unlike Emma's records with Google a few years back, there was no logging of CPU and disk utilization. So we don't have the data to analyze.

 

 

Suboptimal Algorithm Selection:

 

The last performance issue showed up late in the computation and is a bug in y-cruncher. After I was given remote access to the machine and was able to monitor the computation more closely, I noticed that it was often choosing very poor algorithm parameters. The result was a noticeable slow-down on some of the larger operations. While it's also difficult to quantify its effect on the whole computation, it definitely slowed down the final division and square root steps by around 50%.

 

This bug was then fixed for v0.8.4. But I decided not to apply it to this computation since it was nearing completion and it was safer to not touch it anymore than was absolutely necessary.

 

In the end, it's difficult to know how much the computation was slowed down by all these issues. At least not without rerunning it with all the software fixes and hardware adjustments in place. But of course the problems didn't stop with just poor performance...

 

 
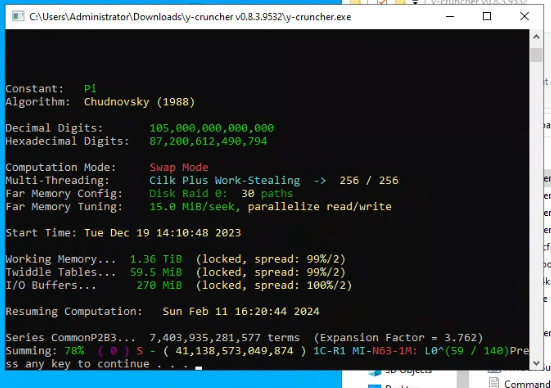
y-cruncher crashes with no error message.

Late Computation Crash:

 

Near the end of the computation, the program mysteriously crashed without an error message. When it was restarted from the last save point, it crashed again at the same place a day later. So the alarm bells started going off because it's clear at this point that there's an issue with the program.

 

To make matters worse:

  1. y-cruncher rarely just *crashes* unless the hardware is very unstable. The fact that it crashed twice in exactly the same spot immediately implies that it is not a hardware instability.
  2. When y-cruncher encounters an error, it's supposed to print an error message. No error was printed.
  3. When y-cruncher crashes on Windows, it catches the fault and creates a minidump file for itself that can be sent to me to debug. It failed to do that as well.

The vast majority of subtle hardware errors do not crash the program. Instead they trigger redundancy check failures which always get printed on the screen. But there was nothing. The application process literally just died.

 

But there was one thing I remembered: In Windows, crash handlers do not work if the crash is from heap corruption. Thus if y-cruncher crashed due to heap corruption, the crash handler that creates its own minidump does not run. Furthermore, early in January, I fixed a bug for v0.8.4 that could cause y-cruncher to crash if an error occurred at the right time.

 

When y-cruncher encounters an error, it throws an exception which is supposed to propagate up the execution stack until it is caught at higher level and printed out. What was happening instead was an async object lifetime bug. The exception causes a premature stack unwind on the thread that owns an object. So the object gets destructed while other threads are still using it. (yeah, typical C++ bs) Thus the use-after-free would corrupt the heap and crash the program - bypassing the crash handler and terminating the progran before it has a chance to print the error message.

 

Cross-checking the exact point of the crash confirms that it was in the right place where this could happen. So that probably explains the silent crash.

 

But what was the original exception? Obviously I wouldn't know until I backported the fix from v0.8.4 to v0.8.3 and reran the computation to the failure spot and (hopefully) have an error message to see this time.

 

(By this point, I had been given full remote access to the machine to do whatever I needed with the machine and the (incomplete) computation. So in addition to the patched binary, the program was now running under a debugger. Because yes, we're going to compute 105 trillion digits of Pi on Windows through the Visual Studio IDE in case of further shenanigans.)

 

But based on the last printed status line, I had a rough idea of where the program was during the error. Thus I kind of already knew what the error message would be. (The dreaded "Coefficient is too large" error.) So I wasn't going to wait a day for the program to hit the error again and troll me with the same message that it trolls overclockers with bad ram. Thus I started looking into the code near the crash and the likely sources of error. While I wasn't expecting to find the actual error, I was at least looking for places to add debugging code.

 

Then after going through many spots, mentally injecting errors, and simulating how the program would fail, I found one spot that matched what was happening. It was deep inside the AVX512 codepath of the N63 multiply algorithm.

 

Without getting into the details of the code and the algorithm that it implemented (since that would require a multi-page blog to cover), there was some floating-point arithmetic that was incorrectly written in a way that led to loss of precision due to destructive cancellation. It was so bad that I still don't understand how it ever worked at all. Yet the code ran correctly in my manual tests, passed weeks and weeks of unit and integration tests, and even passed a bunch of Jordan's recent large computations of other constants. And as luck would have it, it only blew up on a 40 trillion digit multiply while attempting a Pi record.

 

Fast forward 2 more days (with further delays caused by the system getting knocked offline by someone physically bumping into it), the program (with a fix implemented) successfully ran through the failure spot. From there, the rest of the computation finished without further incidents and the digits verified correct.

 

So this bug I found by visual inspection indeed was the bug that was causing all of this. Had this not been the case, things could've gone really bad. 24 hour repro time. $100k+ of hardware being tied up. Half a million lines of code.

 

 

Post Mortem:

 

So what happened? How did I screw this up?

 

Well... Move fast and break things... and get very unlucky.

 

Last year, ~70% of the code relevant to Pi was rewritten. And it all happened in a relatively short amount of time (140,000 lines of code over 9 months).

 

Normally, development is slow and I spend a lot of time validating what I do before moving on. Then there is the implicit (and outsourced) testing of just letting the program soak in the public for a long time while making incremental improvements. Each time someone submits a large run (or a Pi record) it would basically serve as extra validation of what has been done so far.

 

None of this happened last year as basically the entire program was replaced all at once. And because the task was so big, I started getting impatient to see results. So that meant cutting corners with some of the manual validation that normally happens during incremental development. In other words, the rewrites of v0.8.x lacked both the internal and public testing that y-cruncher normally goes through and became too reliant on internal automated testing.

 

In the end, quite a few bugs slipped through - 3 of which showed up in this computation:

The N63 multiply bug is the rather unfortunate one as the relevant code was copy/pasted from elsewhere in the program where it had already been proven correct. But in my haste to get things done, I had not realized that the preconditions had changed in a way that invalided both the proof and the code itself.

 

As luck would have it, the code only breaks on sizes far beyond the scope of the automated tests and far beyond what my own hardware is even capable of. So once the bug was in and I had already moved on to other things, it had no chance of being caught. So someone would've had to find it for me. And that ended up being this 105 trillion digit Pi record attempt.

 

All 3 bugs were part of the newly rewritten code. The Amdahl's Law/Zen4 Hazard predated the rewrite and is not considered a bug as the code was behaving as originally intended. All of these (including the Amdahl's Law/Zen4 Hazard) have been fixed in the latest release (v0.8.4). So hopefully stability will improve going forward.

 

You could argue that "move fast and break things" is the right way to approach things that don't involve human safety. And I would agree - except that I don't have the resources to clean up the resulting mess when things break at such scales. It only worked out this time because Jordan, StorageReview, and the relevant hardware sponsors had the patience to let me use their hardware to sort everything out.

 

 

 

Version 0.8.4 Released: (February 21, 2024) - permalink

 

y-cruncher v0.8.4 has been released with most of the improvements in non-Pi related math as well as continued improvements for large computations in swap mode.

 

For the purpose of competitive benchmarking, v0.8.4 does have changes that theoretically affect performance of the benchmark-relevant computations. But so far I have yet to be able to measure any difference. So until someone proves me wrong, I declare that v0.8.4 benchmarks are comparable to both v0.8.3 and v0.8.2 for both competitive benchmarking and hardware reviews.

 

 

New Math Improvements:

 

Jorge Zuniga has done it again! This time with new fastest formulas for Log(2), Log(3), and Log(5). You can grab the formula files here:

More information on MathOverflow.

 

Log(2) is one of the most fundumental constants and is used in many places such as the AGM algorithm for the logarithm and the Euler-Mascheroni Constant. It has been decades since the last time Log(2) has had a new fastest formula, but Jorge has found one that's 50% faster!

 

y-cruncher v0.8.4 will special-case for these values and will use these formulas instead of the auto-generated ArcCoth() Machin-like formulas.

 

 

And on a somewhat related note, the custom formula feature has gone through some rework and now has some new functionality:

Some of these are convenience wrappers of existing functionality while others are entirely new. And as before, all custom formula functionality supports swap mode with checkpointing and can therefore be taken up to billions/trillions of digits if desired.

 

The main addition is the exponential function exp(x). This has been a notable omission given that log(x) has been supported since first release of the custom formula feature. And now that exp(x) has finally been added, it unlocks the non-integer power function as well as the rest of the hyperbolic trigonometric functions.

 

With that we get a new category of constants. A sample of which include:

I'll note that while y-cruncher supports exp(x), it's rather slow to evaluate. Supporting it at all was more important than making it performance optimal. Nevertheless, it is still quasi-linear in run-time, so you can (in theory) compute exp(x) for non-trivial x to trillions of digits. But it will be a longer wait given the massive implied big-O constant.

 

 

 

Improvements for Large Computations:

 

Now we move onto the same old stuff that's been going on since v0.8.2 - improvements relevant to very large computations.

 

Three main things have changed here:

 

Increasing the Limit from 1 x 1015 digits to 108 x 1015 digits:

 

Historically, y-cruncher has been capped to 1 x 1015 digits. And with the Pi record currently sitting at 100 trillion digits (1 x 1014), it's not hard to imagine the limit being reached in the near future - possibly within a few years.

 

The 1 x 1015 digits comes from what I call the "float-indexing limit". It is the use of double-precision for program "flow control parameters". For example:

Given that double-precision only has around 16 digits of precision, it begins to run out for computations that approach that many digits. And since it's difficult to pin-point exactly when round-off becomes problematic, y-cruncher has been artificially capped at 1015 digits as a safe limit.

 

As of v0.8.4, all uses of "float-indexing" is now done using a higher-precision data type, thus eliminating this limit of 1015 digits. And with one limit removed, the next lowest limit kicks in which (as of this writing) is likely to be 108 x 1015 from the limit of the current 64-bit NTT implementation. Going beyond that gets uncertain as many things begin to overflow 64-bit integers. Fortunately, that will not be a problem for decades to come.

 

 

Checkpointing the Radix Conversion:

 

Moving on... Checkpointing is crucial to large computations because it allows the program to resume a run after being interrupted. Without checkpointing, the recent Pi records wouldn't be achievable as it's virtually impossible to keep a large machine running under stress for so many months without something breaking.

 

For checkpointing to be useful, they must be frequent enough that the computer can easily reach the next checkpoint without failing. If the time between two checkpoints exceeds the MTTF (Mean Time to Failure), it becomes difficult to make forward progress since it'll likely require multiple attempts to cross the gap. For this reason, 90% of y-cruncher does frequent checkpoints.

 

That remaining 10% is the radix conversion. This operation has never supported checkpointing because the algorithm is in-place and destructive. Meaning that it constantly overwrites its own dataset making it difficult to checkpoint because you can't roll back to data that has been overwritten. Over the years, the lack of checkpointing here has become a big enough problem that several of the Pi records have indeed required multiple attempts to get through the conversion. So it has become a liability that is getting worse as the record gets pushed higher and higher.

 

The difficulty of solving this combined with a lot of tech-debt in the implementation meant that I kept procrastinating it for years. And it would require rewriting the algorithm with a completely new approach. As the years went by, the old radix conversion became the last thing that was still using double-precision float-indexing. Thus it got to the point where the old radix conversion was holding back two things: checkpointing and y-cruncher's size limit.

 

So for v0.8.4, I finally bit the bullet and did that much needed redesign+rewrite of the entire swap mode radix conversion.

 

While the new radix conversion supports checkpointing, it still has a higher-than-normal chance of a failure corrupting a checkpoint due the close spatial proximity of data writes to checkpointed data. So in preparation for this, support for multiple levels of checkpointing was added in the previous version (v0.8.3) that will give you multiple points to roll back to in the event of an interruption. For the radix conversion, it means having the option to roll back to before the conversion should the mid-conversion checkpoint become corrupted.

 

 

 

And lastly, the Amdahl's Law and AMD superalignment issue has been fixed. It seems that the problem was worse than I had initially thought. So bad that even Intel servers are sometimes outperforming the AMD ones for large swap mode computations. So this will be a very much welcomed improvement bugfix for AMD servers.

 

 

----

 

 

And that should be it for this release. As with all new releases that touch critical infrastructure, I strongly recommend testing at scale before attempting any long running computation (like a Pi record attempt). My own testing capability is of course limited to the (rather modest) hardware that I personally own. For this release, that piece of "critical infrastructure" is of course the radix conversion.

 

 

Version 0.8.3 Patched: (February 13, 2024) - permalink

 

A new patch for v0.8.3 has been released that fixes a serious bug in the N63 large multiply algorithm. The bug only affects specific versions and binaries.

 

The affected binaries are:

Both Windows and Linux are affected. And can only happen on computations above 29 trillion digits with the likelihood increasing for larger sizes. While this bug affects very few people, it is severe for those who are as it can block record attempts.

 

 

 

FLINT: The Rising Star of Bignum Libraries: (February 9, 2024) - permalink

 

So apparently there's a new crown for the fastest open-sourced bignum library. It is FLINT (Fast Library for Number Theory).

 

Historically, the "main" open-sourced bignum library was GMP which was (and still is) used by everything from computer algebra systems, to Python, to even the GCC compiler. It (along with its fork, MPIR) was also the fastest bignum library out there.

 

In the past, I used to follow both GMP and MPIR. But development on both stagnated around 10 years ago, which caused me to tune out of the field as a whole. And because of that, I completely missed the rise of the FLINT library which seems to have taken the scene by storm.

 

In simple terms, FLINT is a modern bignum library that supports SIMD and parallel computing - the very two things that GMP has failed to embrace. With AVX2, it beats GMP by 3x in raw speed and blows it out once any sort of parallelism is enabled.

 

With GMP left in the dust, the next natural thing to compare it to is... y-cruncher. But to be clear, this is not a fair comparison. FLINT is generic library that can do a zillion things that y-cruncher cannot. And y-cruncher is specialized to do one thing - compute Pi. So they are different programs with different purposes that happen to overlap in some functionality. The fact that we're even here shows how far FLINT has come.

 

So we'll be comparing the following programs:

All 3 programs use the Chudnovsky formula. And all programs include the time needed to convert the digits to decimal representation, but not the time to output or write the digits to disk.

 

The benchmark system is the top-of-the-line desktop Zen4:

All benchmark times are in seconds and are in highlighted in green. Memory usage is also tracked and highlighted in blue.

 

Unless otherwise stated, all benchmarks were run in Ubuntu 22.04.

All computations were done entirely in memory. There is no usage of disk or swap space.

 

 

Pi - 1 thread:

Digits GMP (no GCD) GMP (GCD) FLINT 3.0.1 y-cruncher v0.8.3 (Linux) y-cruncher (Windows)
100,000,000 66.754 1.00 GB 61.727 1.40 GB 31.93 1.01 GB 11.477 452 MB 10.879 452 MB
250,000,000 200.032 2.30 GB 183.011 3.27 GB 87.299 2.68 GB 33.958 1.09 GB 31.462 1.09 GB
1,000,000,000 1,033.029 9.36 GB 907.280 12.2 GB 425.515 11.7 GB 167.279 4.34 GB 157.342 4.34 GB
5,000,000,000 6,941.757 49.6 GB 5,809.793 62.7 GB 2,668.45 54.8 GB 1,076.713 22.3 GB 990.442 22.3 GB
10,000,000,000 15,442.140 99.3 GB 12,920.34 120 GB 5,798.24 109 GB 2,369.535 44.6 GB 2,158.399 44.6 GB
25,000,000,000 Out of Memory Out of Memory Out of Memory 6,568.023 111 GB 6,107.845 111 GB

The first thing we see here is that the GCD optimization gives about 10-20% speedup, but at the cost of 20% higher memory usage. This is why the program has a toggle to enable/disable GCD.

 

FLINT beats GMP by 2-3x. These results are consistent with their own reported benchmarks confirming that I've at least correctly compiled it. And as they mention, FLINT does not do the GCD optimization. A 2-3x gain over the existing state-of-the-art is a huge.

 

With this beatdown of GMP, it brings FLINT within a factor of 3 of y-cruncher. My benchmarks here show a slightly wider gap between FLINT and y-cruncher than what they have. But it is a different machine and I'm not sure if FLINT actually uses AVX512 despite having a flag for it (--enable-avx512). Regardless, AVX512 doesn't bring huge gains over AVX2 on Zen4 for pure floating-point workloads such as the type of algorithm that they are using.

 

For a generic library, this is very impressive as it probably lacks many of the specialized optimizations that y-cruncher does. (though worth noting that y-cruncher also does not do the GCD optimization)

 

Moving over to memory usage, both GMP and FLINT use more than twice the memory that y-cruncher does. This is reasonable since y-cruncher does make a substantial effort reduce its memory usage. (more on this later)

 

So FLINT is looking very good so far. Now let's enable some parallelism...

 

 

Pi - 32 threads:

Digits GMP (no GCD) GMP (GCD) FLINT 3.0.1 y-cruncher v0.8.3 (Linux) y-cruncher (Windows)
100,000,000 23.773 1.25 GB 17.862 1.80 GB 6.386 4.52 GB 1.559 507 MB 1.455 507 MB
250,000,000 65.799 3.32 GB 50.188 4.29 GB 19.438 9.80 GB 4.234 1.15 GB 4.079 1.15 GB
1,000,000,000 317.333 12.4 GB 224.57 16.6 GB 95.201 34.3 GB 19.428 4.40 GB 18.793 4.40 GB
5,000,000,000 2,004.362 51.7 GB 1,312.231 74.6 GB 550.325 138 GB 113.422 22.3 GB 111.467 22.3 GB
10,000,000,000 4,275.017 99.2 GB 2,872.915 141 GB Out of Memory 252.495 44.7 GB 242.246 44.7 GB
25,000,000,000 Out of Memory Out of Memory Out of Memory 714.804 111 GB 683.368 111 GB

As this is a 16-core machine with hyperthreading, the maximum speedup expected would be on the order of 16x. But because of power throttling, turbo limits, and other resource bottlenecks, actual parallel speedups will fall well short of that.

 

The first thing we see here is that y-cruncher scales better than both GMP and FLINT as the performance gap grows to 12x and 5x respectively. From watching the Ubuntu System Monitor, it is obvious that Amdahl's Law is having an effect. Both GMP and FLINT spend significant amounts of time running code that is either not parallelized or is under-parallelized. With such a big loss to Amdahl's Law, it becomes difficult to gauge if any other bottlenecks come into play. Memory bandwidth is the one I was most interested in because that is y-cruncher's achilles heel. Maybe I'll revisit this in the future if/when FLINT is able to approach 100% CPU utilization.

 

But the elephant in the room is FLINT's memory usage - which skyrockets to more than 2x of what GMP needs and 5x of what y-cruncher needs. So while both GMP and y-cruncher manage to avoid blowing up memory when parallelizing, FLINT does not.

 

I didn't try very hard to see what FLINT is doing wrong, but I suspect it may be parallelizing at too high a level. Parallelizing at the highest level of an algorithm tends to result in memory usage that grows linearly with the # of threads until the entire working set is in memory simultaneously.

 

Both the 3rd party GMP Pi implementation and y-cruncher serialize the upper levels of the computation specifically to avoid blowing up memory. But while this approach reduces memory usage, it is not a free optimization and can have negative performance impact. So it's a space-time trade-off.

 

y-cruncher, which is aimed at extremely large computations, tries to strike a balance between speed and memory efficiency. So it trades away some speed to use less memory since it allows bigger computations to be done. Some of the old classic Pi programs like PiFast also do this. PiFast even makes this tunable where you can select how much speed to trade away to reduce memory.

 

 

Euler-Mascheroni Constant - 32 threads:

 

The memory explosion when parallelizing tends to get worse for slower constants. So lets look at the Euler-Mascheroni Constant - which is much slower than Pi.

 

And sure enough, FLINT memory usage spikes to nearly 20x of y-cruncher.

Digits FLINT 3.0.1 y-cruncher v0.8.3 (Linux) y-cruncher (Windows)
10,000,000 9.037 2.35 GB 3.274 243 MB 2.427 243 MB
100,000,000 141.718 14.3 GB 36.999 795 MB 34.928 795 MB
1,000,000,000 2,038.47 138 GB 575.467 7.07 GB 560.219 7.07 GB
10,000,000,000 Out of Memory 7,139.21 68.6 GB 7,005.28 68.6 GB

While this looks pretty bad, it is likely far beyond what FLINT is designed for and thus not on the developer's radar. The Euler-Mascheroni Constant is also far less common than Pi and thus gets much less attention (both in usage and developer time).

 

 

Overall, FLINT has come a long way since the days of GMP's dominance. Pushing it to its limit does reveal some glaring inefficiencies which (if I've correctly accessed them), are probably easy to fix. So while I don't expect FLINT to beat y-cruncher any time soon, it's likely a few easy optimizations away from coming a lot closer.